7 NHST: Paired-Sample t-test and Nonparametric tests

7.1 Overview

In the previous chapters we have looked at one-sample t-tests and between-samples (two-sample) t-tests. In this chapter we will continue to look the paired-sample t-test (sometimes called the dependent sample or within-subject t-test). The paired-sample t-test is a statistical procedure used to determine whether the mean difference between two sets of observations from the same or matched participants is zero.

As in all tests, the paired-sample t-test has two competing hypotheses: the null hypothesis and the alternative hypothesis.

• The null hypothesis assumes that the true mean difference between the paired samples is zero: \[H_0: \mu1 = \mu_2\].
• The alternative hypothesis assumes that the true mean difference between the paired samples is not equal to zero: \[H_1: \mu1 \ne \mu_2\].

In this chapter we are going to look at running the paired-sample t-test, but to begin with we will do a little work on the checks of your data that you need to perform prior to analysis.

Assumptions of tests

So far we have focused your skills on data-wrangling, visualisations, and probability, and now we are moving more towards the actual analysis stage of research. However, as you will know from your lectures, all tests, and particularly parametric tests, make a number of assumptions about the data that is being tested, and that you, as a responsible researcher, need to check these assumptions are "held" as any violation of the assumptions may make your results invalid.

For t-tests the assumptions change for two-sample and paired-sample designs (the one-sample and matched-pairs designs can be thought of as within-subjects designs).

The assumptions of the two-sample t-test are:

• All data points are independent.
• The variance across both groups/conditions should be equal.
• The dependent variable must be continuous (interval/ratio).
  
• The dependent variable should be normally distributed.

And the assumptions of the paired-sample t-test are:

• All participants appear in both conditions/groups.
• The dependent variable must be continuous (interval/ratio).
  
• The dependent variable should be normally distributed.

Before beginning any analysis, using your data-wrangling skills, you must check to see if the data deviates from these assumptions, and whether it contains any outliers, in order to assess the quality of the results. If assumption violation are present, you may want to use nonparametric tests instead.

In this chapter we will:

• Run assumption checks
• Analyse an experiment with a paired-sample design.
• Understand when and how to run nonparametric tests.

7.2 The Paired-Sample t-test

Up to now we have covered the one-sample t-test and the between-subjects/two-sample t-test, and we have talked a little about the assumptions of the between-subjects t-test. We are now going to expand on that by looking at the final t-test we need to cover, the paired-sample/within-subject t-test; used when you have the same participants in both conditions, or you have two groups of people that are very closely matched on various demographics such as age, IQ, verbal acuity, etc.

In exploring the paired-sample t-test we will also look more at checking the assumptions of t-tests. If you refer back to the earlier activities you will know that many of the assumptions of the different t-tests are largely similar (apart from equal variance, for example), so by looking at these assumption check here you can apply them to other tests.

For this activity we will look at a replication of Furnham (1986) that the School of Psychology & Neuroscience, University of Glasgow, carried out in 2016-2017. It would be worth familiarising yourself with the original study at some point for more information regarding the concepts of the study, but it is not essential in order to complete the exercises: Furnham, A. (1986), The Robustness of the Recency Effect: Studies Using Legal Evidence. We will explain a little about the study before carrying out some tasks to check the assumptions and to analyse the data.

7.2.1 Data Set: Juror Decision Making

The research question in this experiment is: Does the order of information affect juror judgments of guilt or innocence? Thus, the overall aim of the original experiment was to investigate whether the decision a jury member makes about the innocence or guilt of a defendant could be influenced by something as simple as when crucial evidence is presented during a trial. During the experiment participants (Level 2 Psychology students) listened to a series of recordings that recreated the 1804 trial of a man known as Joseph Parker who was accused of assuming two identities and marrying two women; i.e. bigamy. Each participant listened to the same recordings of evidence, presented by both prosecution and defense witnesses, and were asked to judge how guilty they thought Mr. Parker was at 14 different time points during the experiment on a scale of 1 to 9: 1 being innocent and 9 being guilty. The 14 time points came immediately after certain pieces of evidence.

The manipulation in the experiment was that the order of evidence was altered so that half the participants received one order of evidence and the other half received the second order of evidence. Key to the order change was the time at which a critical piece of evidence was presented. This critical evidence proved that the defendant was innocent. The Middle group heard this evidence at Timepoint 9 of the trial whereas the Late group heard this evidence at Timepoint 13. You will have an opportunity to look at all the data in due course but, for today's exercise, we will only focus on the Late group.

In this exercise, your task is to analyse the data to examine whether the participants' ratings of guilt significantly changed before and after the presentation of the critical evidence in the Late condition. If the critical evidence, which proved the defendant's innocence, had the desired effect then you should see a significant drop in ratings of guilt after hearing this evidence (Timepoint 13) compared to before (Timepoint 12). Or in other words, we hypothesised that there would be a significant decrease in ratings of guilt, caused by presentation of the critical evidence, from Timepoint 12 to Timepoint 13.

7.2.2 Task 1: Load the data

• Download the data for this experiment from here.
• Unzip the data and save it into a folder you have access to and set that folder as your working directory.
• Open a new R Markdown document.
• Today you will need the broom and tidyverse libraries. Load these in this order. Remember that the order you load in libraries matters.
• Using read_csv(), load in the data from the experiment contained in GuiltJudgements.csv and store it in a tibble called ratings.

7.2.3 Task 2: Wrangle the data

As above, you are only interested in the 75 participants of the Late group here and only for Timepoints 12 (rating before key evidence) and 13 (rating after key evidence). But having had a look at ratings you will see that the Timepoints are in wide format (columns 1 to 14 - each a different timepoint) and the Evidence column contains the Middle group as well. Let's do some wrangling to make the data look like it is shown in Table 7.1 below. The steps to do this are as follows:

1. filter() only those participants from the Late condition.

2. select() only the Timepoints 12 and 13.

3. rename() these Timepoints as Twelve and Thirteen as numerical names are hard to deal with.

4. pivot_longer() to gather the data so that you have the below structure. (Note: here only the first four rows are shown as an example).

5. Do this all as one pipe and store it in a tibble called lates. Your tibble, lates will have 150 rows and 4 columns.

Check that your table looks like the table below.

Table 7.1: How your table should look from Task 2

Participant	Evidence	Timepoint	GuiltRating
1	Late	Twelve	7
1	Late	Thirteen	5
2	Late	Twelve	5
2	Late	Thirteen	3

1. You need to specify the column you want to filter from, stating which variable (i.e. Late) that this column is ‘equal to’ (i.e. ‘==’)

2. Other than the two columns representing Timepoints 12 and 13, there are two other columns you need to keep in order to identify the participant and group. Use the table as a guide.

3. When renaming, first state the new variable name and then designate this to the old variable name. i.e. rename(data, new_column_name = old_column_name). If the old column is a number, put it in backticks, e.g. Five = backtick 5 backtick (but be sure to use `s).

4. The structure shown has two new columns: Timepoint and GuiltRating, which are both created from columns Twelve to Thirteen. You should state these new column names when using pivot_longer(), as well as the columns you used to create them. Think about completing this: cols = X:Y, names_to = "Where", values_to = "Where"

Quickfire Questions

• To check you have completed this Task correctly, enter the appropriate values into the boxes.
  • This dataset has: columns by rows and participants.

7.2.4 Task 3: Look at the histogram for normality

We are now going to show you how to start checking data in terms of assumptions such as normality. We will do this through creating some visualisations of the data and thinking about what these visualisations tell us about the data. First we will create a histogram for each of the two timepoints to see if their individual distributions appear normally distributed.

• Use your data visualisation skills to plot a histogram for each TimePoint. Have the two histograms side-by-side in the one figure and set the histogram binwidth to something reasonable for this experiment.

1. ggplot() + geom_?

2. A histogram only requires you to state aes(x) and not aes(x, y). We are examining the differences in guilt rating scores across participants. Which column from lates should be ‘x’? It should be your categorical Independent Variable.

3. binwidth is an argument you can specify within geom_histogram() such as geom_historgram(binwidth = ...). Think about an appropriate binwidth. Your guilt rating scale runs from 1 to 9 in increments of 1.

4. You have used something like facet_?() to display a categorical variables (i.e. Timepoint) according to the different levels it contains. You need to specify the variable you want to use, using ~ before the variable name.

5. Beyond this point, you can think about adding appropriate labels and color if you like.

7.2.5 Task 4: A boxplot of outliers

We can also check for outliers in the different conditions. Outliers can obviously create skewed data and make the mean value misleading.

• Create a boxplot for each Timepoint by GuiltRating and check for outliers.

1. This time when using ggplot() to create a boxplot, you need to specify both ‘x’, which is the discrete/categorical variable, and ‘y’, which is the continuous variable.

2. • geom_boxplot() - see Chapter 3 for an example.

Quickfire Questions

• How many outliers do you see? 0 1 2 3 too many to count

Remember that outliers are normally represented as dots or stars beyond the whiskers of the boxplot. As you will see in the solution the data contains an outlier. We won't deal with outliers today, but it is good to be able to spot them at the moment. It would be worth thinking about how you could deal with outliers. There are numerous methods such as replacing with a given value or removing the participants. Remember though that this decision, how to deal with outliers, and any deviation from normality, should be considered and written down in advance as part of your preregistration protocol.

7.2.6 Task 5: The violin-boxplot

Boxplots and histograms tell you slightly different information about the same data, which we will discuss in a minute, and you are developing your skills of plotting and interpreting them. But we have already introduced you to a new type of figure that can combine the information from a boxplot and a histogram into the one figure. We do this using a violin-boxplot.

• Take the code you've written above for the boxplot (Task 4) and add on geom_violin as another layer. You may need to rearrange your code (i.e., the boxplot and violin plot functions) so that the violin plots appear underneath the boxplots. Think layers of the visualisation!

• ggplot() works on layers - the first layer (i.e., the first plot you call) is underneath the second layer. This means that to get a boxplot showing on top of a violin plot, the violin must come first (i.e., you need to call geom_violin() before you call geom_boxplot())

• We have embellished the figure a little in the solution that you can have a look at once you have the basics sorted. Things like adding a width call to the boxplot, or an alpha call to the violin.

Do you see how the violin-boxplot relates to the histogram you created earlier? In your head, rotate your histograms so that the bars are pointing to the left and imagine there is a mirror-image of them (making a two-sided histogram). This should look similar to your violin-boxplot. Be sure to be able to still locate the outlier in the Thirteen condition.

HOLD ON!!!

As you will know from your lectures on the assumptions of a paired-sample t-test, when dealing with a within-subjects design, and a paired t-test, normality is actually determined based on the difference between the two conditions. That is, we should in fact check that the distribution of the scores of the difference between the two conditions is normally distributed. We have been looking at it in terms of separate conditions, to some degree to show you the process of the visualisations, but to really follow the paired-sample t-test we need to look at the normality of the difference. The code below will create a violin-boxplot visualisation of the difference between the two conditions and you should now be able to understand this code.

Have a look at the output, and at the code, and think about whether the scores of the difference between the two conditions is normally distributed.

Note: In the code below, outliers will appear as red circles and individual data points will appear as blue Xs. Can you see what is controlling this? Why is this an important step? We will say why in a second, but it is worth thinking about yourself for a minute or two.

lates %>% 
  spread(Timepoint, GuiltRating) %>%
  mutate(diff = Thirteen - Twelve) %>%
  ggplot(aes(x = Evidence, y = diff)) +
  geom_violin() +
  geom_boxplot(fill = "red", 
               width = .5, 
               alpha = .1, 
               outlier.colour = "red") +
  geom_jitter(color = "blue", 
              width = .1, 
              shape = 4) + 
  theme_classic()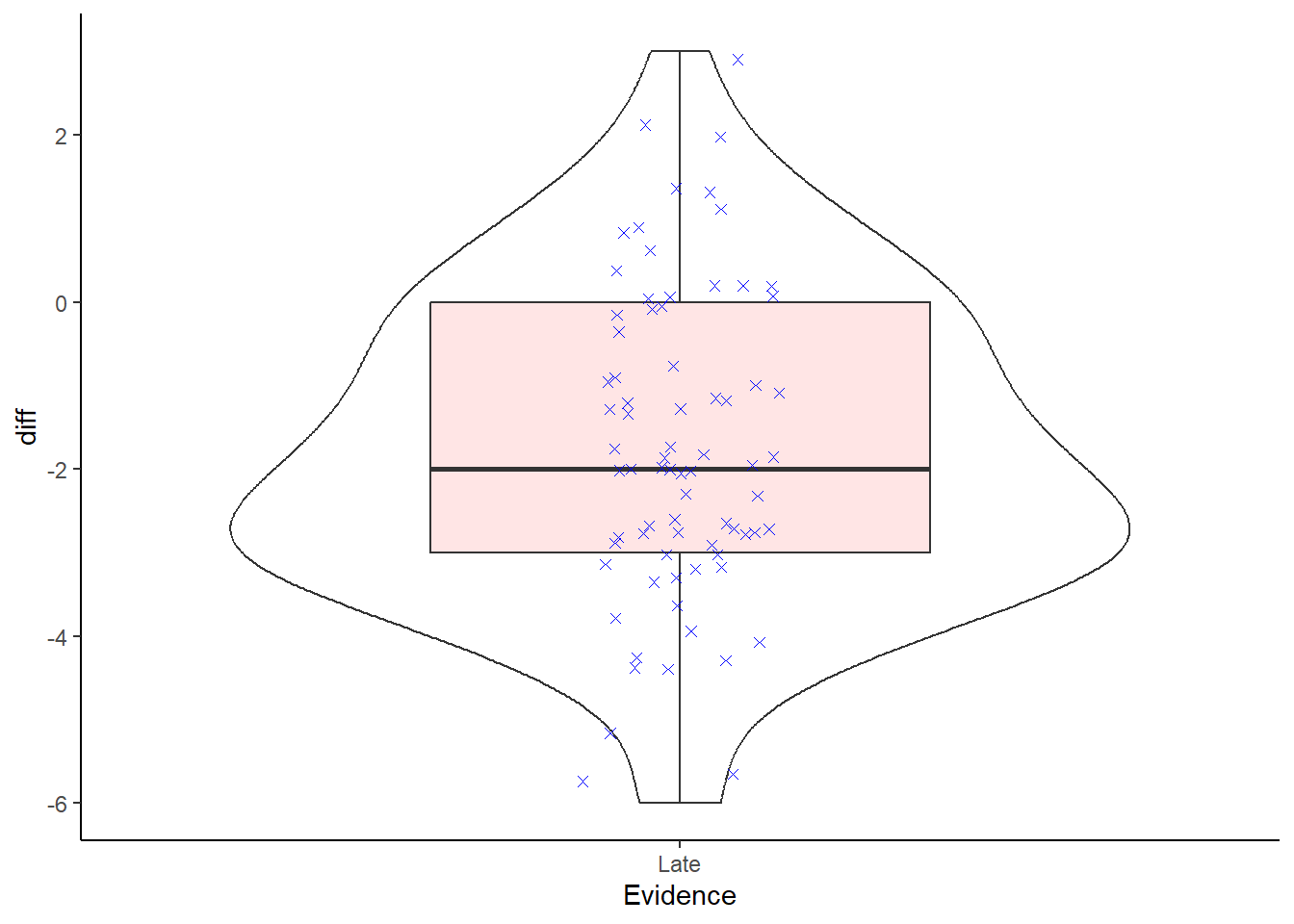

Figure 7.1: A violin-boxplot showing the distribution of the scores of the difference between the Thirteen and Twelve conditions. Individual participant data show as blue stars. Positive values would indicate that the rating in the Thirteen condition is higher than the rating in the Twelve condition. Outliers will show as red circles.

Thinking Cap Point

We have now checked our assumptions, but we sort of still need to make a decision regarding normality. Having had a look at the figures we have created, spend a few minutes thinking about whether the data is normally distributed or not.

Also, think about why this data shows no outliers, but the individual conditions did show an outlier. Lastly, why is it important to code different presentations of outliers from the individual data points?

Is the data normally distributed or not?

What you are looking for is a nice symmetry around the top and bottom half of the violin-boxplot. You are looking for the median (thick black line) to be roughly in the middle of the boxplot, and the whiskers of the boxplot to be roughly equal length. If the median is closer to the box’s lower values and the upper whisker is longer, then the data is positively skewed. If the median is closer to the box’s higher values and the lower whisker is longer, then the data is negatively skewed.

Also, you want the violin to have a bulge in the middle of the figure and to taper off at the top and at the bottom. You also want to have just one bulge on the violin (symbolising where most of the scores are). Two bulges in the violin may be indicative of two different response patterns or samples within the one dataset.

Now we need to make our judgement on normality. Remember that real data will never have the textbook curve that the normal distribution has. It will always be a bit messier than that and to some degree a judgement call is needed or you need to use a test to compare your sample distribution to the normal distribution. Tests such as the Kolmogorov-Smirnov and the Shapiro-Wilks tests are sometimes recommended to determine violation from a normal distribution. However, these last two tests are not that reliable depending on sample size and often we revert back to the judgement call. Again, it is really important that steps are documented, so a future researcher can check and confirm the process.

Overall, the data look normally distributed - at least visually (albeit with a slight positive skew).

Outliers vs Data Points?

You have to be careful when using geom_jitter() to show individual data points. You can overcomplicate a figure and if you have a large number of participants then it might not make sense to include the individual data points as it can just create a noisy figure. A second point is that you want to make sure that your outliers are not confused with individual data points; all outliers are data points, but not all data points are outliers. So, in order not to confuse data and outliers, you need to make sure you are properly controlling the colors and shapes of different information in a figure. And be sure to explain in the figure legend what each element shows.

Lastly, you will have noted that when we plotted the original violin-boxplot for the individual conditions, the Thirteen group had an outlier. However, now when we plot the difference as a violin-boxplot we see no outliers. This is important and reinforces why you have to plot the correct data in order to check the assumptions. The assumptions for a paired-sample t-test is based on the difference between the scores of individual participants. What we see here is that when we calculate the difference of scores there is no outlier, even though the original data point was an outlier. That is fine within consideration of the assumption - as the assumption only looks at the difference. That said, you might also want to check that the original outlier was an acceptable value on the rating scale (e.g., between 1 and 9) and not some wild value that has come about through bad data entry (e.g., a rating of 13; say if the rating and the condition got mixed up somehow).

Great. We have run some data checks on the assumptions of the paired-sample t-test. We checked the data for normal distribution, using a violin-boxplot, looking for skewed data and outliers. And from our understanding of the data, and of arguments in the field, whilst the rating scale used could be called ordinal, many, including Furnham treat it as interval. Finally, we haven't spotted any issues in our code to suggest that any participant didn't give a response in both conditions, but we can check that again in the descriptives - both conditions should have an n = 75.

We will do that check and also run some descriptives to start understanding the relationship between the two levels of interest: Timepoint 12 and Timepoint 13.

7.2.7 Task 6: Calculating Descriptives

• Calculate the mean, standard deviation, and Lower and Upper values of the 95% Confidence Interval (CI) for both levels of the Independent Variable (the two time points). You will need to also calculate the n() - see Chapter 2 - and the Standard Error to complete this task. Store all this data in a tibble called descriptives.
  
• The solution shows the values you should obtain, but be sure to have a go first. Be sure to confirm that both groups have 75 people in it!
• Answering these questions may help on calculating the CIs:

Quickfire Questions

• From the options, which equation would use to calculate the LowerCI? mean - 1.96 * sd mean * 1.96 - se mean - 1.96 * se mean * 1.96 - sd
• From the options, which equation would use to calculate the UpperCI? mean + 1.96 * sd mean * 1.96 + se mean + 1.96 * se mean * 1.96 + sd

1. group_by() the categorical column Timepoint. This is the column you want to compare groups for.
2. summarise()
3. Different calculations can be used within the same summarise() function as long as they are calculated in the order which you require them. For example, you first need to calculate the participant number, n = n(), and the standard deviation, sd = sd(variable), in order to calculate the standard error, se = sd/sqrt(n), which is required to calculate your Confidence Intervals.
4. For the 95% Confidence Interval, you need to calculate an LowerCI and a UpperCI using the appropriate formula. Remember it will be mean + 1.96se and mean - 1.96se. If you don’t include the mean then you are just calculating how much higher and lower than the mean the CI should be. We want the actual interval.

Let’s think about your task. You’re looking to calculate the 95% Confidence Interval for normally distributed data. To do this you require a z-score which tells you how many standard deviations you are from the mean. 95% of the area under a normal distribution curve lies within 1.96 standard deviations from the mean; i.e. 1.96 SD above and below the mean.

If you were looking to calculate a 99% Confidence Interval you would instead use a z-score of 2.576. This takes into account a greater area under the normal distribution curve and so you are further away from the mean (i.e., closer to the tail ends of the curve), resulting in a higher z-score.

7.2.8 Task 7: Visualising Means and Descriptives

• Using the data in descriptives, produce a plot that visualises the mean and 95% Confidence Intervals.
  • One way would be a basic barplot, shown in previous chapters, with error bars indicating the 95% CI.
  • To add the error bars you could add a layer like below.
  • Feel free to embellish the figure as you see fit.
  • We have shown a couple of options in the solution that you should look at and try adjusting, after you have tried your own plot.

geom_errorbar(aes(ymin = LowerCI, ymax = UpperCI),
              position = "dodge", width = .15)

• We recommend using geom_col()
• Remember to add (+) the geom_errorbar() line above to your code! Don’t pipe it.
• In the above code for error bars, the aesthetic, aes(), allows you to set the min and max values of the error bars - these will be the max and min of your CIs.
• position = "dodge" does the same as position = position_dodge() and position = position_dodge(width = .9). There are a number of ways to use a position call and they all do the same thing.

Important to remember: As we have mentioned in previous labs, barplots are not that informative in themselves. Going ahead in your research, keep in mind that you should look to use plots that incorporate a good indication of the distribution/spread of the individual data points as well, when needed. Barplots give a good representation on categorical counts like in a chi-square test, but not so much on ordinal or interval data where there is likely to be a spread.

Thinking Cap Point

Now that we have some descriptives to look at we need to think what they tell us - or really how we interpret them. First thing is to think back to the hypothesis as every interpretation is phrased around the hypothesis. We hypothesised that there would be a significant decrease in ratings of guilt, caused by presentation of the critical evidence, from Timepoint 12 to Timepoint 13. Do you think there will be a significant difference between the two time points? What evidence do you have? Think about the overlap of confidence intervals! Remember the key thing at this stage is that it is a subjective impression - "It appears that there might be...." or words to that effect.

7.2.9 Task 8: The paired-sample t-test

Now we have checked our assumptions and ran our descriptives, the last thing we need to do is to perform the paired-sample t-test to test the differences between the two time points.

To perform the paired-sample t-test you use the same t.test function as you did in Chapter 6. However, this time you add the argument, paired = TRUE, as this is what tells the code "yes, this is a paired-sample t-test".

• Perform a paired-sample t-test between guilt ratings at the crucial time points (Twelve and Thirteen) for the participants in the Late group. Store the data (e.g., tidy) in a tibble called results.

From your work in earlier chapters you will know two ways to use the t.test() function. The two options are:

The formula approach

• t.test(x ~ y, data, paired = TRUE/FALSE, alternative ="two.sided"/"greater"/"less")
• where x is the columns containing your DV and y is typically your grouping variable (i.e., your independent variable).

The vector approach

• t.test(data %>% filter(condition1) %>% pull(data),data %>% filter(condition2) %>% pull(data), paired = TRUE)

• To pull out the Twelve and Thirteen columns to pass as condition1 and condition2, you can use: lates %>% pull(Twelve) and lates %>% pull(Thirteen).

Regardless of method

• Do not forget to state paired = TRUE or you will run a between-subjects t-test

• Once you’ve calculated results, don’t forget to tidy() - you can add this using a pipe!

• If you don’t quite understand the use of tidy() yet, run your t.test() without tidy() and see what happens!

• Note: Both options of running the t-test will give the same result. The only difference will be whether the t-value is positive or negative. Remember that the vector approach allows you to state what is condition 1 and what is condition 2. The formula approach just runs conditions in alphabetical or numerical order.

Thinking Cap Point

Now look at the output of your test within the tibble results. In your group, spend some time breaking down the results you can see. Do you understand what all the values mean and where they come from? You may have to match up some of your knowledge from your lectures. Was there a significant difference or not? We are about to write it up so best we know for sure.

7.2.10 Task 9: The Write-up

Fill in the blanks below to complete this paragraph, summarising the results of the study. You will need to refer back to the information within results and descriptives to get the correct answers and to make sure you understand the output of the t-test.

• Enter all values to two decimal places and present the absolute t-value.
• The solutions contain a completed version of this paragraph for you to compare against.

"A paired-sample t-test one-sample t-test between-samples t-test matched-pairs t-test was ran to compare the change in guilt ratings before (M = , SD = ) and after (M = , SD = ) the crucial evidence was heard. A significant non-significant difference was found (t() = , p = .05 > .05 = .001 < .001) with Timepoint 13 having an average rating units lower than Timepoint 12. This tells us that the critical evidence did have an influence on the rating of guilt by jury members that the critical evidence did not have an influence on the rating of guilt by jury members that the critical evidence and the rating of guilt by jury members are unconnected something but I am not quite sure right now, I best check!`

• t-tests take the following format: t(df) = t-value, p = p-value

• your results states degrees of freedom as parameter, and your t-value as statistic.

• estimate is your mean difference between ratings at Timepoints Twelve and Thirteen.

• The conf.low and conf.high values are the 95% Confidence Intervals for the mean difference between the two conditions. We haven’t included them in the write-up here but you could do. This could be written as something like, “there was a difference between the two groups (M = -1.76, 95% CI = [-2.19, -1.33])”.

Two tips:

• If you were to write up the above for a future report, you can make your write-up reproducible as well by using the output of your tibbles and calling specific columns. For example, t(`r results$parameter`) = `r results$statistic %>% abs()`, p < .001, when knitted will become t(74) = 8.23, p < .001. So, code can prevent mistakes in write-ups! However, working with rounding up p-values can be tricky and we have offered a code in the solutions to show you how.

• Another handy function when writing up is the round() function for putting values to a given number of decimal places. For example in the above if we wanted to round the absolute t-value to two decimal places we might do results %>% pull(statistic) %>% abs() %>% round(2) which would give t = 8.23. Or maybe we want three decimal places: results$statistic %>% abs() %>% round(3) which would give t = 8.232. So really handy function and follows the format of round(value_to_round, number_of_decimal_places).

Excellent work! You can see how performing the t-test is only a small part of the entire process: wrangling the data, calculating descriptives, and plotting the data to check the distributions and assumptions is a major part of the analysis process. Over the past chapters, you have been building all of these skills and so you should be able to see them being put to good use now that we have moved onto more complex data analysis. Running the inferential part is usually just one line of code.

7.3 Practice Your Skills

Using the data from above, perform a paired-sample t-test for the Middle group where the crucial evidence was presented on Timepoint 9. Save your current .Rmd file, then make a copy of it, rename it accordingly, and go through the steps for the Middle group. Since this exercise is very close to the example we worked through in this chapter, we have not added the solutions in the end. Feel free to check with your peers and discuss if there is a difference in ratings of guilt, caused by presentation of the critical evidence, from Timepoint 8 to Timepoint 9?

7.4 Non-Parametric tests

In this and previous chapters we have really been focusing on between-subjects and within-subjects t-tests which fall under the category of parametric tests. One of the main things you will know about these tests is that they have a fair number of assumptions that you need to check first to make sure that your results are valid. We looked at how to do this in the main body of the chapter, and you will get more practice at this as we progress, but one question you might have is, what do you do if the assumptions aren't met (or are "violated"" as it is termed)?

So what options are there? There are tests known as non-parametric tests that have fewer assumptions than the parametric tests and can be run quite quickly using the same approach as we have seen with the t-tests. The non-parametric "t-tests" generally don't require any assumption of normality and tend to work on either the medians of the data (as opposed to the mean values) or the rank order of the data - i.e., what was the highest value, the second highest, the lowest - as opposed to the actual value.

And just like there is slightly different versions of t-tests there are different non-parametric tests for between-subjects designs and within-subjects designs:

• The Mann-Whitney U-test is the non-parametric equivalent of the between-subjects t-test
• The Wilcoxon Signed-Ranks Test is the non-parametric equivalent of the within-subjects t-test.

Note: The Mann-Whitney and the Wilcoxon Signed-Ranks tests are now a bit antiquated as they were designed to be done by hand when computer processing power was limited. However, they are still used in Psychology and you will still see them in older papers, so it is worth seeing one in action at least.

So for example, if you were concerned that your data was far from being normally distributed, you might use the Mann-Whitney or the Wilcoxon Signed-Ranks Test depending on your design. Here we will run through a Mann-Whitney U-test and then you can try out a Wilcoxon Signed-Ranks Test in your own time as it uses the same function - it is again just a matter of saying paired = TRUE.

7.4.1 Our Scenario

• Aim: To examine the influence of perceived reward on problem solving.
• Procedure: 14 Participants in 2 groups (7 per group) are asked to solve a difficult lateral thinking puzzle. One group is offered a monetary reward for completing it as quick as possible. One group is offered nothing; just the internal joy of getting the task completed and correct.
• Task: The participants are asked to solve the following puzzle. "Man walks into a bar and asks for a glass of water. The barman shoots at him with a gun. The man smiles, says thanks, and leaves. Why?"
• IV: Reward group vs. No Reward group
• DV: Time taken to solve puzzle measured in minutes.
• Hypothesis: We hypothesise that participants who are given a monetary incentive for solving a puzzle will solve the puzzle significantly faster, as measured in minutes to solve the puzzle, than those that are given no incentive.

7.4.2 Assumption check

Here is our data and a boxplot of the data to try and visualise what is happening in the data.

Table 7.2: Table showing the time taken to complete the puzzle for the Reward and No Reward groups

Participant	Group	Time
1	No Reward	1.32
2	No Reward	3.56
3	No Reward	7.55
4	No Reward	8.05
5	No Reward	8.54
6	No Reward	10.18
7	No Reward	15.55
8	Reward	3.25
9	Reward	5.54
10	Reward	7.66
11	Reward	9.02
12	Reward	10.45
13	Reward	13.21
14	Reward	21.37

## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
## of ggplot2 3.3.4.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.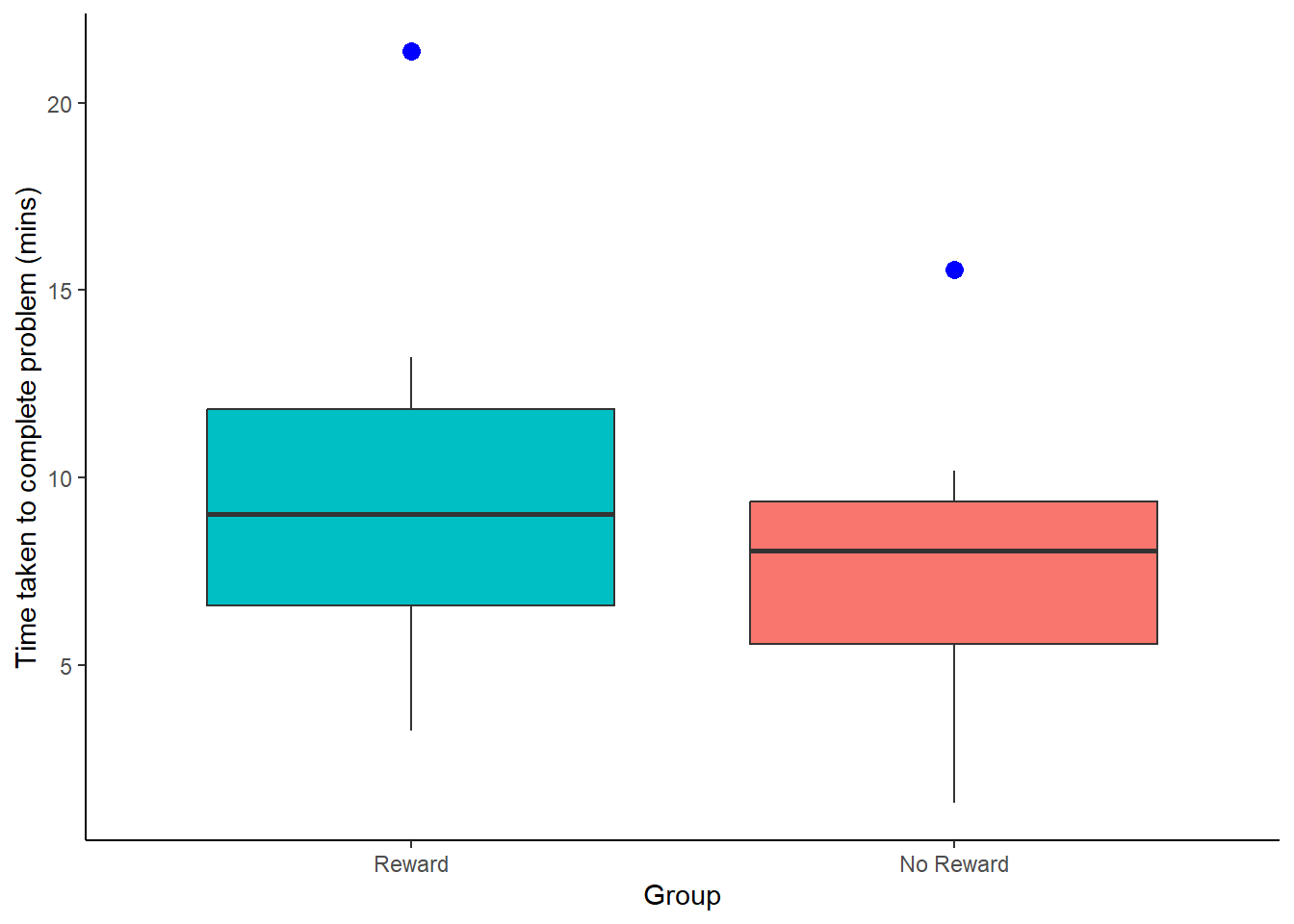

Figure 7.2: Boxplots showing the time taken to solve the puzzle for the two conditions, Reward vs No Reward. Outliers are represented by solid blue dots.

Looking at the boxplots there is potentially some issues with skew in the data (see the No Reward group in particular) and both conditions are showing as having at least one outlier. As such we are not convinced our assumption of normality is held so we will run the Mann-Whitney U-test - the non-parametric equivalent of the two-sample t-test (i.e., independent groups) - as it does not require the assumption of normal data.

7.4.3 The descriptives

Next, as always, we should look at the descriptives as well to make some subjective, descriptive inference about the pattern of the results. One thing to note is that the Mann-Whitney analysis is based on the "rank order" of the data regardless of group. In this code and table below we have put the data in order from lowest to highest and added on a rank order column. We have used the rank() function to create the ranks and setting the ties.method = "average". We won't go into why that is the case here but you can read about it through ?rank.

scores_rnk <- scores %>%
  arrange(Time) %>%
  mutate(ranks = rank(Time, ties.method = "average"))

Table 7.3: Table showing the time taken to complete the puzzle for the Reward and No Reward groups and the rank order of these times.

Participant	Group	Time	ranks
1	No Reward	1.32	1
8	Reward	3.25	2
2	No Reward	3.56	3
9	Reward	5.54	4
3	No Reward	7.55	5
10	Reward	7.66	6
4	No Reward	8.05	7
5	No Reward	8.54	8
11	Reward	9.02	9
6	No Reward	10.18	10
12	Reward	10.45	11
13	Reward	13.21	12
7	No Reward	15.55	13
14	Reward	21.37	14

Here is a table of descriptives for this dataset and the code we used to create it.

ByGrp <- group_by(scores_rnk, Group) %>%
  summarise(n_Pp = n(),
            MedianTime = median(Time),
            MeanRank = mean(ranks))

Table 7.4: Descriptive (N, Medians and Mean Ranks) for the two groups (Reward vs No Reward) in time taken to solve the puzzle.

Group	n_Pp	MedianTime	MeanRank
No Reward	7	8.05	6.714286
Reward	7	9.02	8.285714

Based on figure and descriptive data, we can suggest that there appears to be no real difference between the two groups in terms of time taken to solve the puzzle. The group that was offered a reward have a slightly higher spread of data than the no reward group. However, the medians and mean ranks are very comparable.

7.4.4 Running the inferential test

We will now run the Mann-Whitney U-test to see if the difference between the two groups is significant or not. To do this, somewhat confusingly, we us the wilcox.test() function. The code to do the analysis on the current data (with the tibble scores, the DV in the column Time, and the IV in the column Group) is shown below. It works just like the t-test() function in that you can use either vectors or the formula approach.

Note:

• There are a couple of additional calls in this function that you can read about using the ?wilcox.test() approach.
• We could just have easily used scores_rnk as our tibble in the wilcox.test() as opposed to scores. We are using scores to show you that you don't need to put the ranks into the wilcox.test() function, it will create them itself when it runs the analysis. We only created them to run some descriptives.

result <- wilcox.test(Time ~ Group, 
                      data = scores, alternative = "two.sided", 
            exact = TRUE, correct = FALSE) %>%
  tidy()

And here is the output of the test after is has been tidied into a tibble using tidy()

Table 7.5: Output of the Mann-Whitney U-test

statistic	p.value	method	alternative
19	0.534965	Wilcoxon rank sum exact test	two.sided

The main statistic (the test-value) of the Mann-Whitney U-test is called the U-value and is shown in the above table as statistic; i.e. U = 19 and you can see from the results that the difference was non-significant as p = 0.535.

Note:

• The eagle-eyed of you will spot that the test actually says it is a Wilcoxon rank sum test. That is fine. The Mann-Whitney U-test is calculated from the sum of the ranks (shown in the table above). The Wilcoxon rank sum test is just that, a sum of the ranks. The U-value is then created from the summed ranks.
  
• Don't mistake the Wilcoxon rank sum test mentioned here - for between-subjects - with the Wilcoxon Signed-Ranks test for within-subjects mentioned above. They are different tests.

However, one thing to note about the U is that it is an unstandardised value - meaning that it is dependent on the values sampled and it can't be compared to other U values to look at the magnitude of one effect versus another. The second thing to note about the U-value is that wilcox.test() will return a different U-value depending on which condition is stated as Group 1 or Group 2.

Compare the outputs of these two tests where we have switched the order of the conditions:

Version 1:

result_v1 <- wilcox.test(scores %>% filter(Group == "Reward") %>% pull(Time),
                         scores %>% filter(Group == "No Reward") %>% pull(Time),
                         data = scores, alternative = "two.sided",
                         exact = TRUE, correct = FALSE) %>%
  tidy()

Version 2:

result_v2 <- wilcox.test(scores %>% filter(Group == "No Reward") %>% pull(Time),
                         scores %>% filter(Group == "Reward") %>% pull(Time),
                         data = scores, alternative = "two.sided",
                         exact = TRUE, correct = FALSE) %>%
  tidy()

The U-value for these two tests are, for Version 1, U = 30 and for Version 2, U = 19. This may seem odd, but actually both those test are correct. However, strictly speaking the U-value is the smaller of the two-values given by the different outputs. It is to do with how the U-value is calculated. Both groups have a U-value and the one that is checked for significance is the smaller of the two.

Because U is an unstandardised value, when we present the Mann-Whitney U-test we usually also give a Z-statistic, which is the standardised version of the U-value. We also present an effect size, commonly r.

Z and r can be calculated as follows:

• Z = \(\frac{U - \frac{N1 \times N2}{2}}{\sqrt\frac{N1 \times N2 \times (N1 + N2 + 1)}{12}}\)

• r = \(\frac{Z}{\sqrt(N1 + N2)}\)

Putting these formulas into a coded format would look like this:

U <- result$statistic
N1 <- ByGrp %>% filter(Group == "Reward") %>% pull(n_Pp)
N2 <- ByGrp %>% filter(Group == "No Reward") %>% pull(n_Pp)
Z <- (U - ((N1*N2)/2))/ sqrt((N1*N2*(N1+N2+1))/12)
r <- Z/sqrt(N1+N2)

And as such the write-up could be written as:

The time taken to solve the problem for the Reward group (n = 7, Mdn Time = 9.02, Mean Rank = 8.29) and the no reward group (n = 7, Mdn Time = 8.05, Mean Rank = 6.71) were compared using a Mann-Whitney U-test. No significance difference was found, U = 19, Z = -0.703, p = 0.535, r = -0.188

7.4.5 Last point on calculating U and reporting the test

In the final write-up there we know, because of our codes, that U = 19 is the smallest U-value of the test. However had you put the alternative U, U = 30, when you calculated Z you would have got Z = 0.703, as opposed to Z = -0.703. So your standardised statistic will have the same value but just the opposite polarity (either positive or negative). That is fine though as you can look at the medians and mean ranks to make sure you are interpreting the data correctly.

However, what you do have to watch out for when writing up this test is that you are presenting the correct U-value - remembering that technically you should present the smallest of the two U-values (refer back to Version 1 and Version 2 of using the wilcox.test()) above. Fortunately you don't have to run both analyses to figure out which is the smaller U (though you could if you wanted). There is a quicker way using the below formula:

\(U1 + U2 = N1 \times N2\)

• where U1 is the U-value from your wilcox.test() function
• N1 is the number of people in one group (technically doesn't matter which group) and N2 is the number of people in the other group.

We actually know both our U-values as we ran both tests; they are U1 = 30 and U2 = 19, and we know our two groups are N1 = 7 and N2 = 7. And if we put those numbers in the formula we get

\(U1 + U2 = N1 \times N2\)

=> \(30 + 19 = 7 \times 7\)

=> \(49 = 49\)

So both sides equal 49. But say you only know one of the U-values; you of course will know both Ns. Well you can quickly figure out the other U-value based on:

\(U2 = (N1 \times N2) - U1\)

for example, if you know U1 = 19, N1 = 7 and N = 7 then:

\(U2 = (7 \times 7) - 19\)

=> \(U2 = (49) - 19\)

=> \(U2 = 30\)

And then you just have to present the smallest of the two U-values, in this case U = 19.

Hopefully you now have a decent understanding of the Mann-Whitney test. You could also try running a Wilcoxon Signed-Ranks Test as well though you might have to read a little on how to present those. It is similar to the Mann-Whitney though and you should be able to get there.

Oh, and last last point, how to remember which test is which? Is the Mann-Whitney for between-subjects or within-subjects, and what is the Wilcoxon Signed-Ranks test for? You know they do different designs, but which is which? Well, as silly as this memory aid is: The other name of between-subjects designs, as you know, is independent designs. Add to that the fact that the late great singer Whitney Houston once starred in "The Bodyguard" which was about maintaining your right to freedom and independence. So whenever you get stuck on knowing which test is which, remember Whitney wanted independence in "The Bodyguard" and you should be ok. We did not say this was a very good memory aid!

7.5 Solutions to Questions

Below you will find the solutions to the questions for the Activities for this chapter. Only look at them after giving the questions a good try and speaking to the tutor about any issues.

7.5.1 The Paired-Sample t-test

7.5.1.1 Task 1

library(broom)
library(tidyverse)

ratings <- read_csv("GuiltJudgements.csv")

Return to Task

7.5.1.2 Task 2

lates <- ratings %>%
  filter(Evidence == "Late") %>% 
  select(Participant, Evidence, `12`, `13`) %>% 
  rename(Twelve = `12`, Thirteen = `13`) %>%
  pivot_longer(cols = Twelve:Thirteen, 
               names_to = "Timepoint", 
               values_to = "GuiltRating")

• If you have carried this out correctly, lates will have 150 rows and 4 columns. This comes from 75 participants giving two responses each - TimePoint 12 and TimePoint 13.

Return to Task

7.5.1.3 Task 3

lates %>% 
  ggplot(aes(GuiltRating)) +
  geom_histogram(binwidth = 1) +
 facet_wrap(~Timepoint) +
  labs(x = "GuiltRating", y = NULL) +
theme_bw()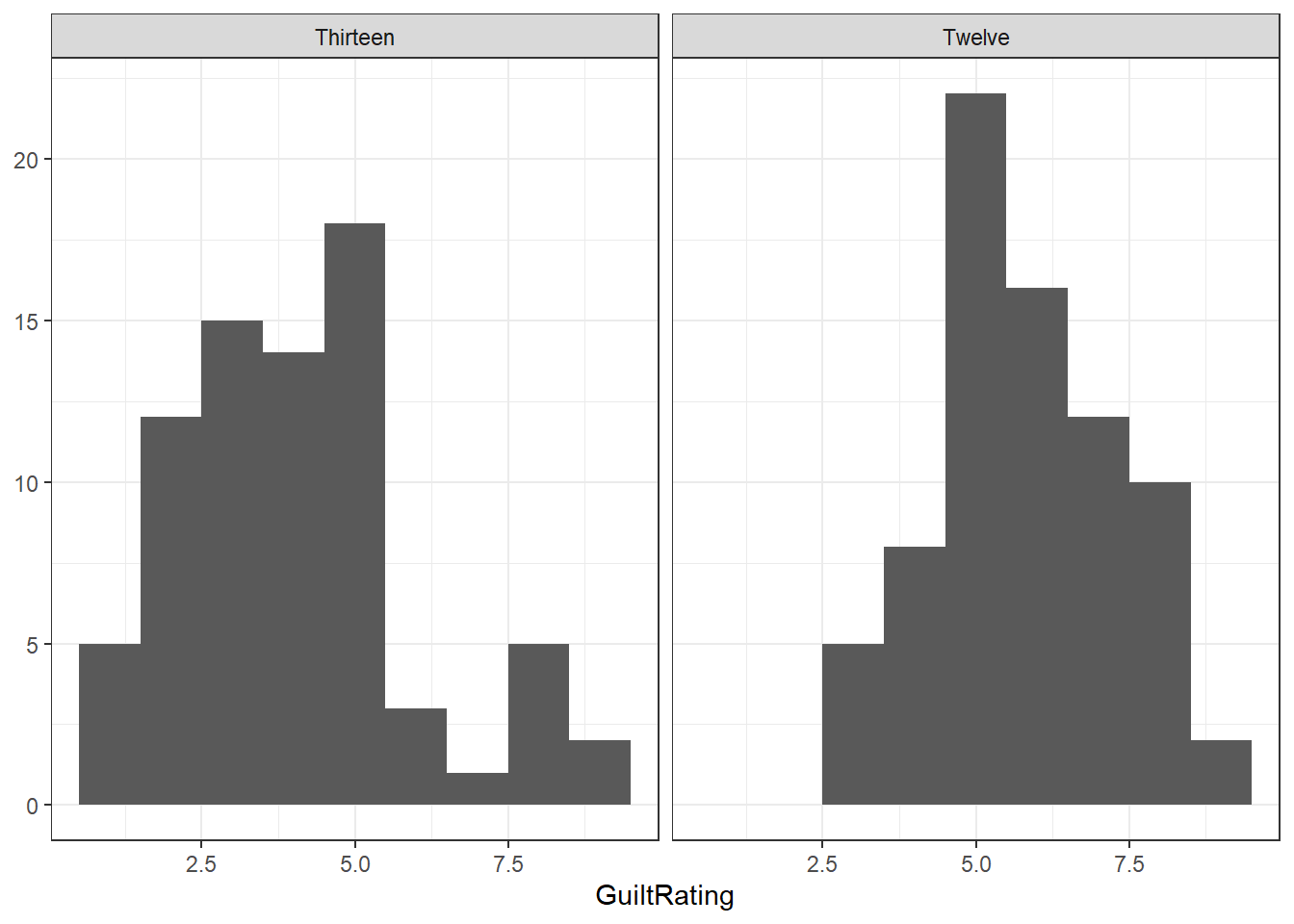

Figure 7.3: Potential Solution to Task 3

Return to Task

7.5.1.4 Task 4

The Task only asks for the boxplot. We have added some additional functions to tidy up the figure a bit that you might want to play with.

lates %>% 
  ggplot(aes(x = Timepoint,
             y = GuiltRating)) + 
  geom_boxplot() +
  scale_y_continuous(breaks = c(1:9)) + 
  coord_cartesian(xlim = c(.5, 2.5), ylim = c(1,9), expand = TRUE) +
  theme_bw()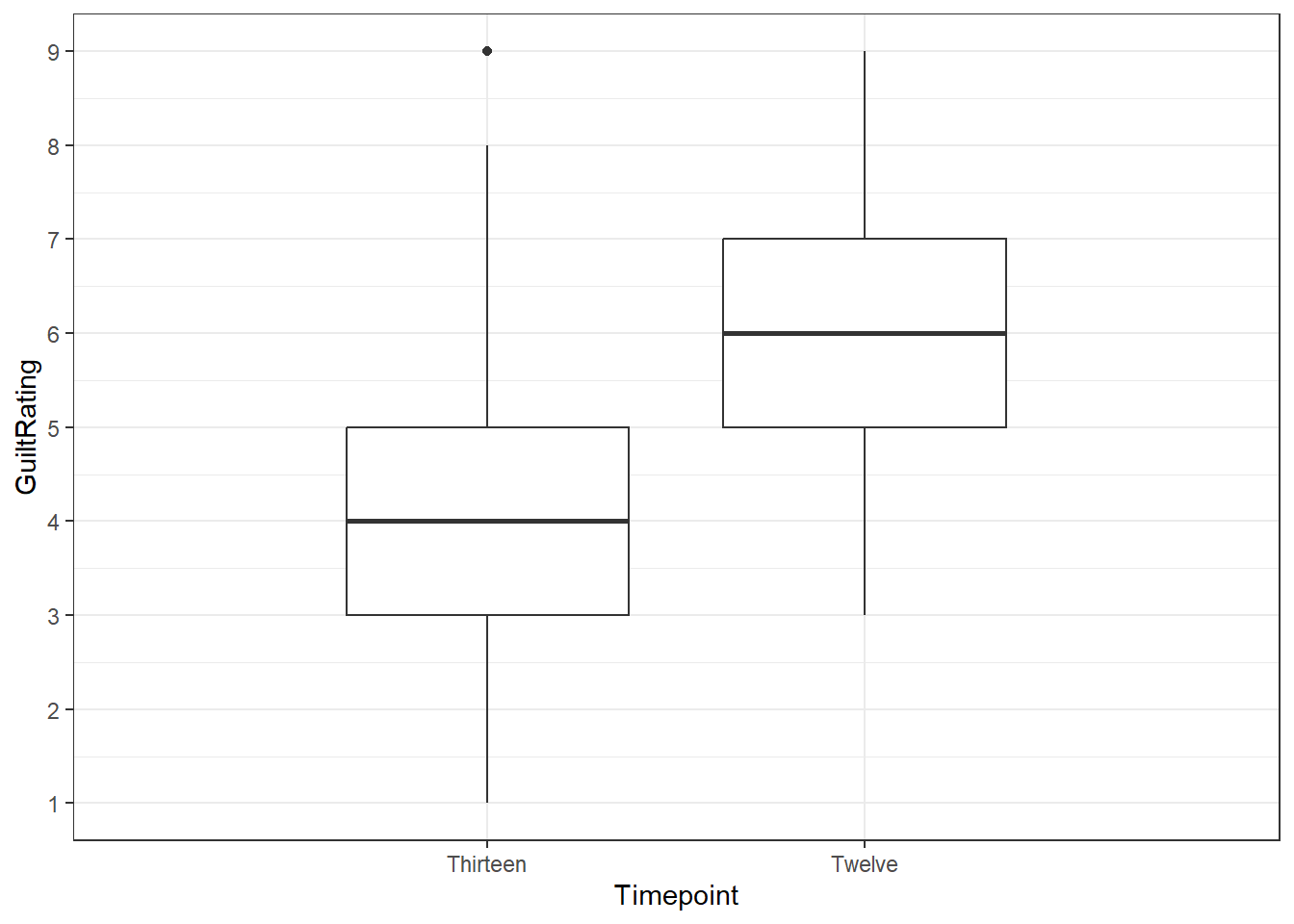

Figure 7.4: Potential Solution to Task 4

You can see that there is one outlier in the Thirteen condition. It is represented by the the single dot far above the whiskers of that boxplot.

Return to Task

7.5.1.5 Task 5

We have added color but that was not necessary:

lates %>% 
  ggplot(aes(x=Timepoint,y=GuiltRating))+
  geom_violin(aes(fill = Timepoint), alpha = .2) + 
  geom_boxplot(width = 0.5) +
  scale_y_continuous(breaks = c(1:9)) + 
  coord_cartesian(ylim = c(1,9), expand = TRUE) +
  theme_bw()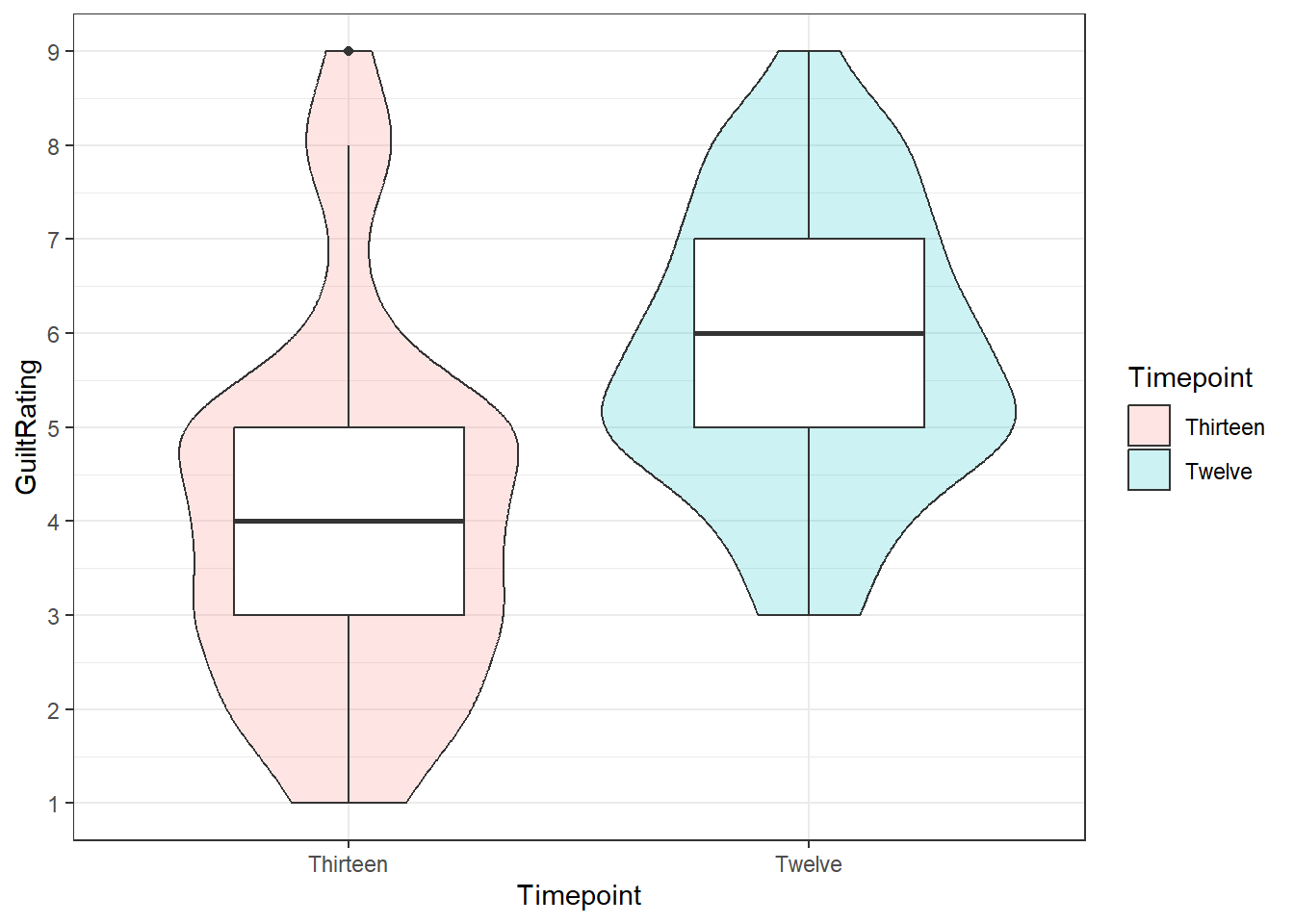

Figure 7.5: Potential Solution to Task 5

• You can still see the outlier at the top of the figure as a solid black dot.

You could even add the geom_jitter to have all the data points:

lates %>% 
  ggplot(aes(x=Timepoint,y=GuiltRating))+
  geom_violin(aes(fill = Timepoint), alpha = .2) + 
  geom_boxplot(width = 0.5) +
  geom_jitter(aes(fill = Timepoint), width = .1, alpha = .2) + 
  scale_y_continuous(breaks = c(1:9)) + 
  coord_cartesian(ylim = c(1,9), expand = TRUE) +
  theme_classic()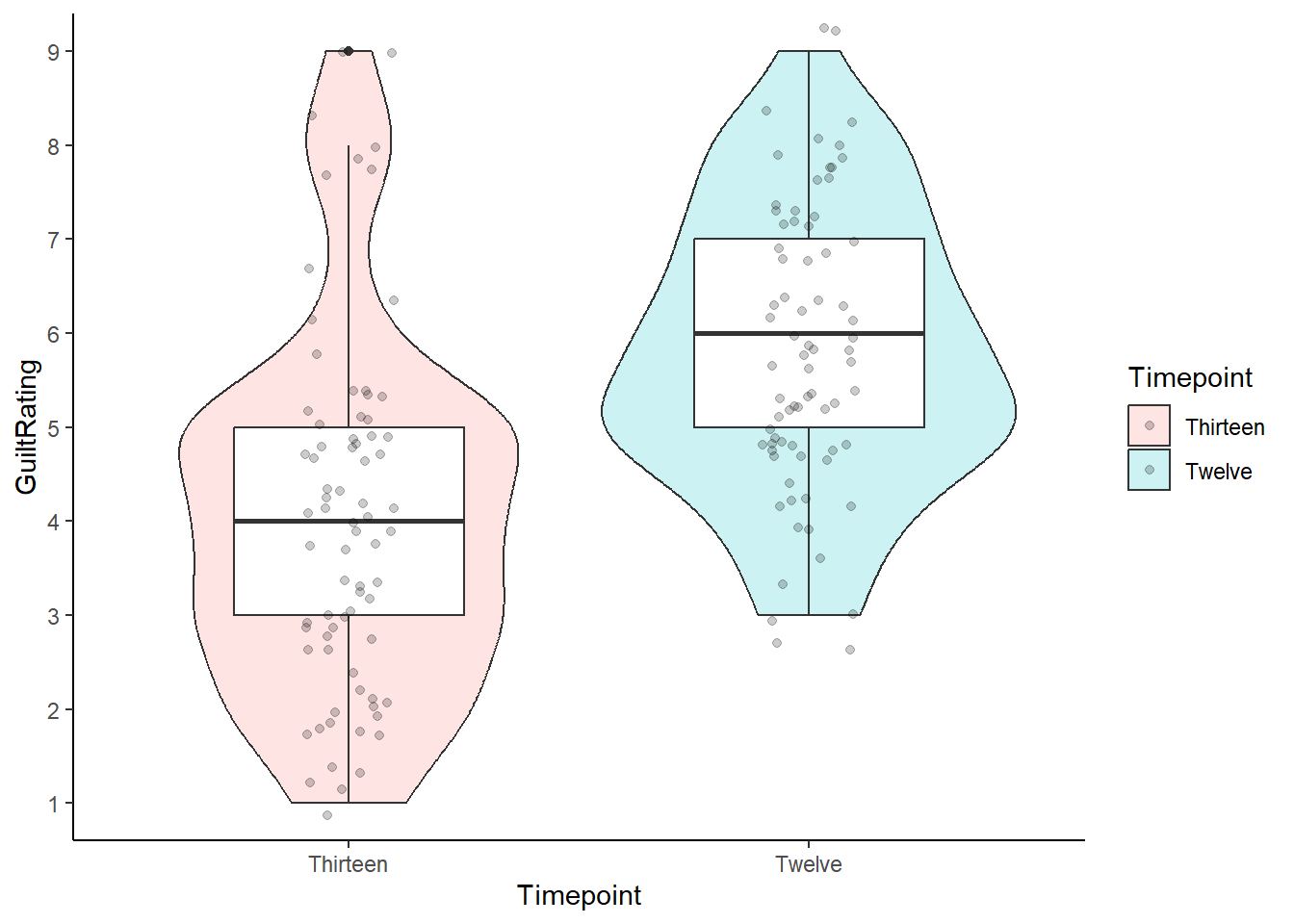

Figure 7.6: Alternative Potential Solution to Task 5

Return to Task

7.5.1.6 Task 6

descriptives <- lates %>% 
  group_by(Timepoint) %>%
  summarise(n = n(),
            mean = mean(GuiltRating),
            sd = sd(GuiltRating),
            se = sd/sqrt(n),
            LowerCI = mean - 1.96*se,
            UpperCI = mean + 1.96*se)

This would show the following data:

knitr::kable(descriptives, align = "c", caption = "Descriptive data for the current study")

Table 7.6: Descriptive data for the current study

Timepoint	n	mean	sd	se	LowerCI	UpperCI
Thirteen	75	4.04	1.934327	0.2233569	3.602221	4.477779
Twelve	75	5.80	1.497746	0.1729448	5.461028	6.138972

Return to Task

7.5.1.7 Task 7

• A basic barplot with 95% Confidence Intervals.
• We have embellished the figure a little but you can mess around with the code to see what each bit does.

ggplot(descriptives, aes(x = Timepoint, y = mean, fill = Timepoint)) + 
  geom_col(colour = "black") +
  scale_fill_manual(values=c("#999000", "#000999")) +
  scale_x_discrete(limits = c("Twelve","Thirteen")) +
  labs(x = "Timepoint of Evidence", y = "GuiltRating") +
  guides(fill="none") +
  geom_errorbar(aes(ymin = LowerCI, ymax = UpperCI),
                position = "dodge", width = .15) +
  scale_y_continuous(breaks = c(1:9), limits = c(0,9)) +
  coord_cartesian(ylim = c(1,9), xlim = c(0.5,2.5), expand = FALSE) +
  theme_classic()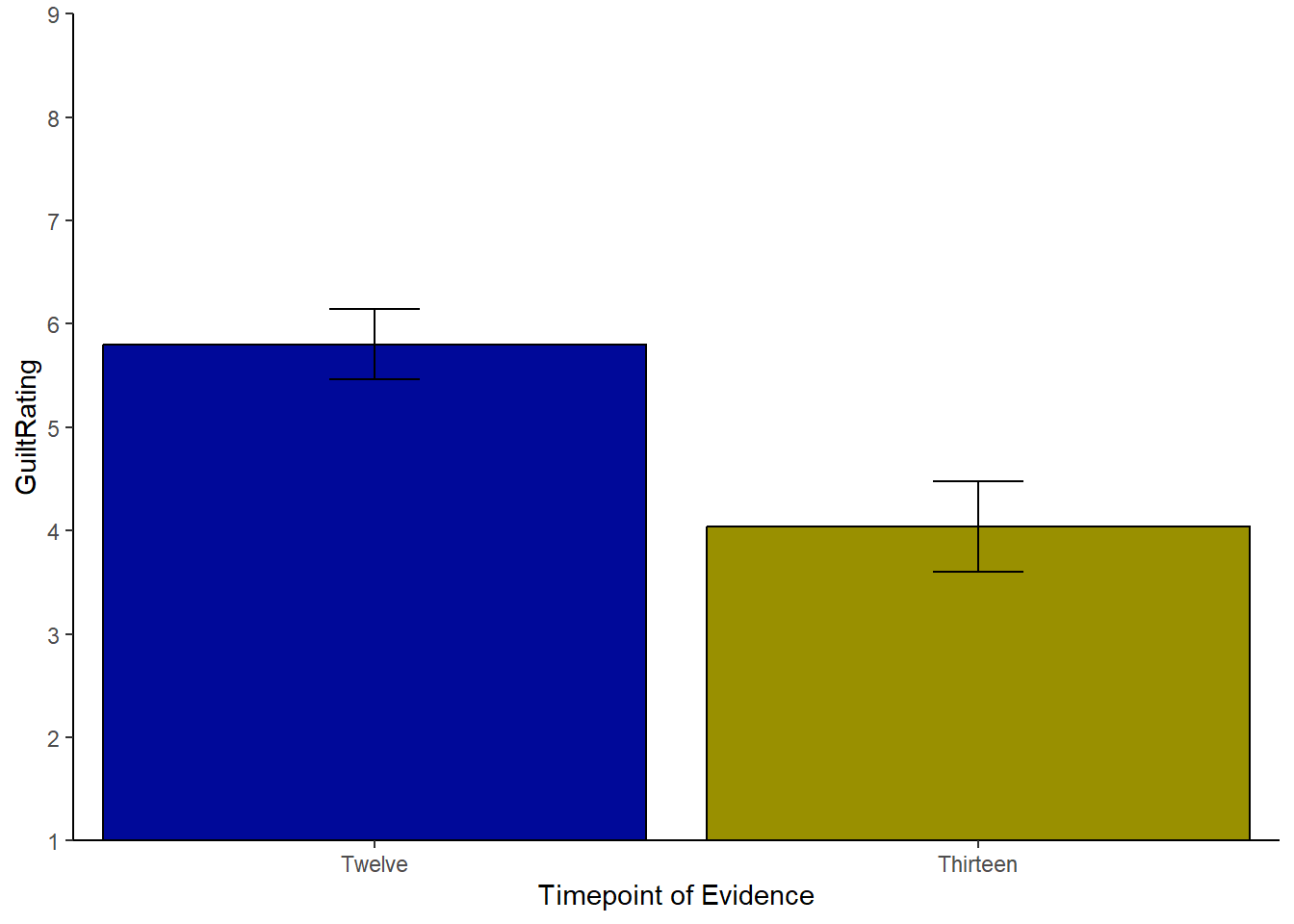

Figure 7.7: Possible Solution to Task 7

• One thing to watch out for with the above code is the scale_y_continuous() function which helps us set the length and tick marks (-) on the y-axis. Rather oddly, if you set the limits = ... to the same values as the ylim = ... in coord_cartesian() then your figure will behave oddly and may disappear. coord_cartesian() is a zoom function and must be set within the limits of the scale, set by scale_y_continuous().

• An alternative way to display just the means and errorbars would be to use the pointrange approach. This image shows again the 95% CI

ggplot(descriptives, aes(x = Timepoint, y = mean, fill = Timepoint)) + 
  geom_pointrange(aes(ymin = LowerCI, ymax = UpperCI))+
  scale_x_discrete(limits = c("Twelve","Thirteen")) +
  labs(x = "Timepoint of Evidence", y = "GuiltRating") +
  guides(fill="none")+
  scale_y_continuous(breaks = c(1:9), limits = c(0,9)) +
  coord_cartesian(ylim = c(1,9), xlim = c(0.5,2.5), expand = FALSE) +
  theme_bw()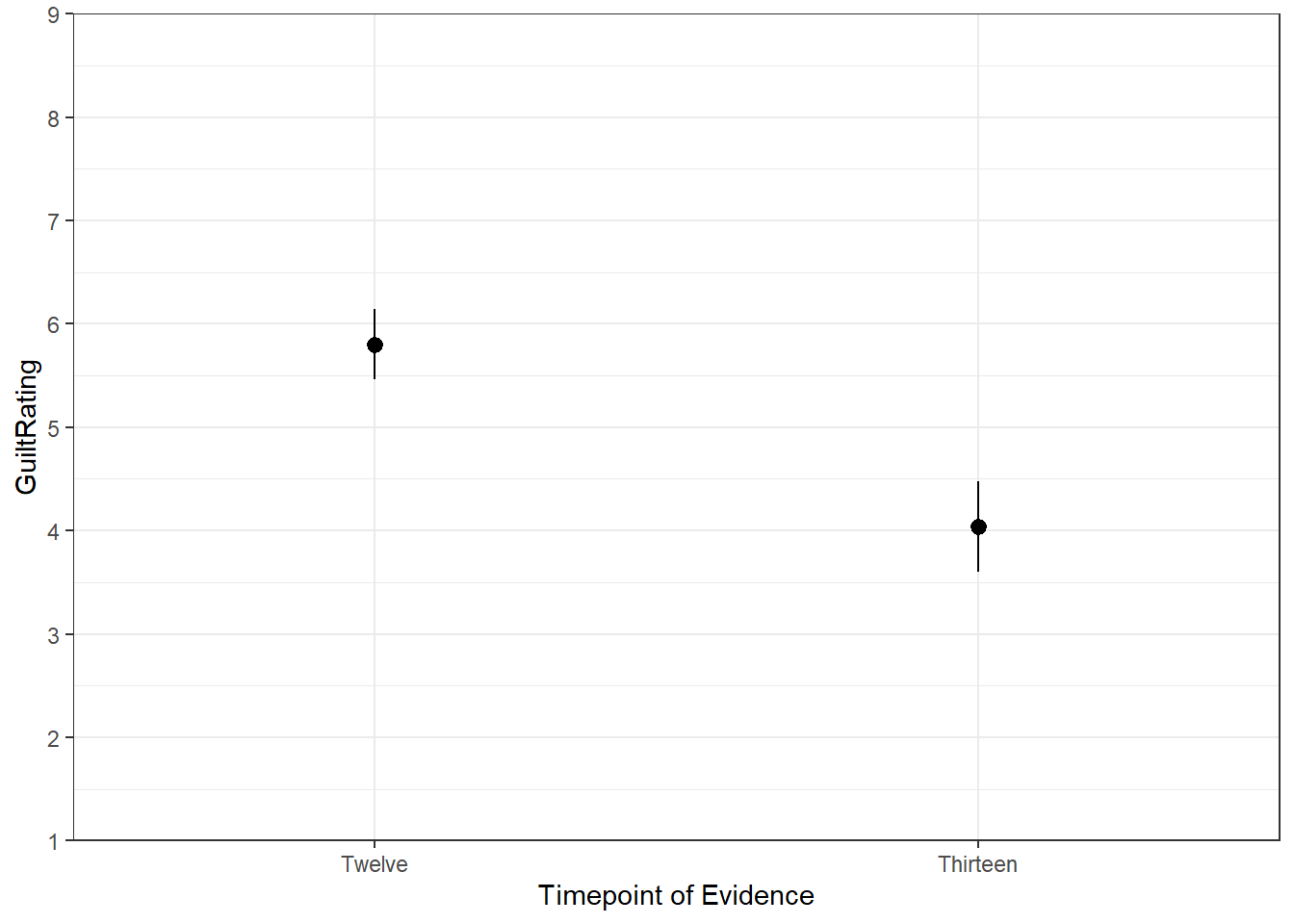

Figure 7.8: Alternative Solution to Task 7

Return to Task

7.5.1.8 Task 8

• Remember to set paired = TRUE to run the within-subjects t-test

results <- t.test(GuiltRating ~ Timepoint, 
                  data = lates, 
                  paired = TRUE, 
                  alternative = "two.sided") %>% tidy()

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
-1.76	-8.232202	0	74	-2.185995	-1.334005	Paired t-test	two.sided

• Alternatively, using the filter() and pull() functions to make force in a given condition as the first condition. Here, below, we are forcing condition Thirteen as the first condition and so the values match the above approach. If you forced condition Twelve as the first condition then the only difference would be that the t-value would change polarity (positive to negative or vice versa).

results <- t.test(lates %>% filter(Timepoint == "Thirteen") %>% pull(GuiltRating),
                  lates %>% filter(Timepoint == "Twelve") %>% pull(GuiltRating),
                  paired = TRUE, 
                  alternative = "two.sided") %>% tidy()

estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
-1.76	-8.232202	0	74	-2.185995	-1.334005	Paired t-test	two.sided

The reason that the two outputs are the same is because the formula (top) method (x ~ y) is actually doing the same process as the second approach, but you are just not sure which is the first condition. This second approach (bottom) just makes it clearer.

Note: The conf.low and conf.high values are the 95% Confidence Intervals for the mean difference between the two conditions. This could be written as something like, "there was a difference between the two groups (M = -1.76, 95% CI = [-2.19, -1.33])".

Return to Task

7.5.1.9 Task 9

A potential write-up for this study would be as follows:

"A paired-samples t-test was ran to compare the change in guilt ratings before (M = 5.8, SD = 1.5) and after (M = 4.04, SD = 1.93) the crucial evidence was heard. A significant difference was found (t(74) = 8.23, p = 4.7113406^{-12}) with Timepoint 13 having an average rating 1.76 units lower than Timepoint 12. This tells us that the critical evidence did have an influence on the rating of guilt by jury members."

Working with rounding p-values

When rounding off p-values that are less than .001, rounding will give you a value of 0 which is technically wrong - the probability will be very low but not 0. As such, and according to APA format, values less than .001 would normally be written as p < .001. To create a reader-friendly p-value, then you could try something like the following in your code:

ifelse(results$p.value < .001, 
       "p < .001", 
       paste0("p = ", round(results$p.value,3))) 

So instead of writing t(74) = 8.23, p = 4.7113406^{-12}, you would write t(74) = 8.23, p < .001

The in-line coding for these options would look like:

p = `r results %>% pull(p.value)` for p = 4.7113406^{-12}

&

`r ifelse(results$p.value < .001, "p < .001", paste0("p = ", round(results$p.value,3)))` for p < .001

Return to Task

Chapter Complete!