8  Paired t-test

Intended Learning Outcomes

By the end of this chapter you should be able to:

  • Compute a paired t-test and effectively report the results.
  • Understand when to use a non-parametric equivalent of the paired t-test, compute it, and report the results.

Individual Walkthrough

8.1 Activity 1: Setup

In this chapter, we will continue working with the dataset from the study by Zwaan et al. (2018). Have a look at Chapter 7 or the SupMats document if you need a refresher on the Simon Task data.

  • Open last week’s project
  • Create a new .Rmd file and save it to your project folder
  • Delete everything after the setup code chunk (e.g., line 12 and below)

8.2 Activity 2: Library and data for today

Today, we will need the following packages rstatix, tidyverse, qqplotr, lsr, and pwr. You should have all the necessary packages installed from previous chapters already. If not, you can install them via the console (see Section 1.5.1 for more details).

Again, load the rstatix package before tidyverse. Then read in the data from MeansSimonTask.csv and the demographics information from DemoSimonTask.csv.

# load in the packages
???

# read in the data
zwaan_data <- ???
zwaan_demo <- ???
# load in the packages
library(rstatix)
library(tidyverse)
library(qqplotr)
library(lsr)
library(pwr)

# read in the data
zwaan_data <- read_csv("MeansSimonTask.csv")
zwaan_demo <- read_csv("DemoSimonTask.csv")

As usual, take some time to familiarise yourself with the data before starting the within-subjects t-test.

Today, we will focus on the Simon effect itself. Remember that the Simon effect predicts shorter response times for congruent trials compared to incongruent trials. Therefore, we are inclined to propose a directional hypothesis.

  • Potential research question: “Is there a significant difference in response times between congruent and incongruent trials in a Simon task?”
  • Null Hypothesis (H0): “There is no significant difference in response times between congruent and incongruent trials in a Simon task.”
  • Alternative Hypothesis (H1): “Response times for congruent trials are significantly shorter than those for incongruent trials in a Simon task.” or phrased differently “Participants will respond significantly faster in congruent trials than in incongruent trials in a Simon task.”

8.3 Activity 3: Preparing the dataframe

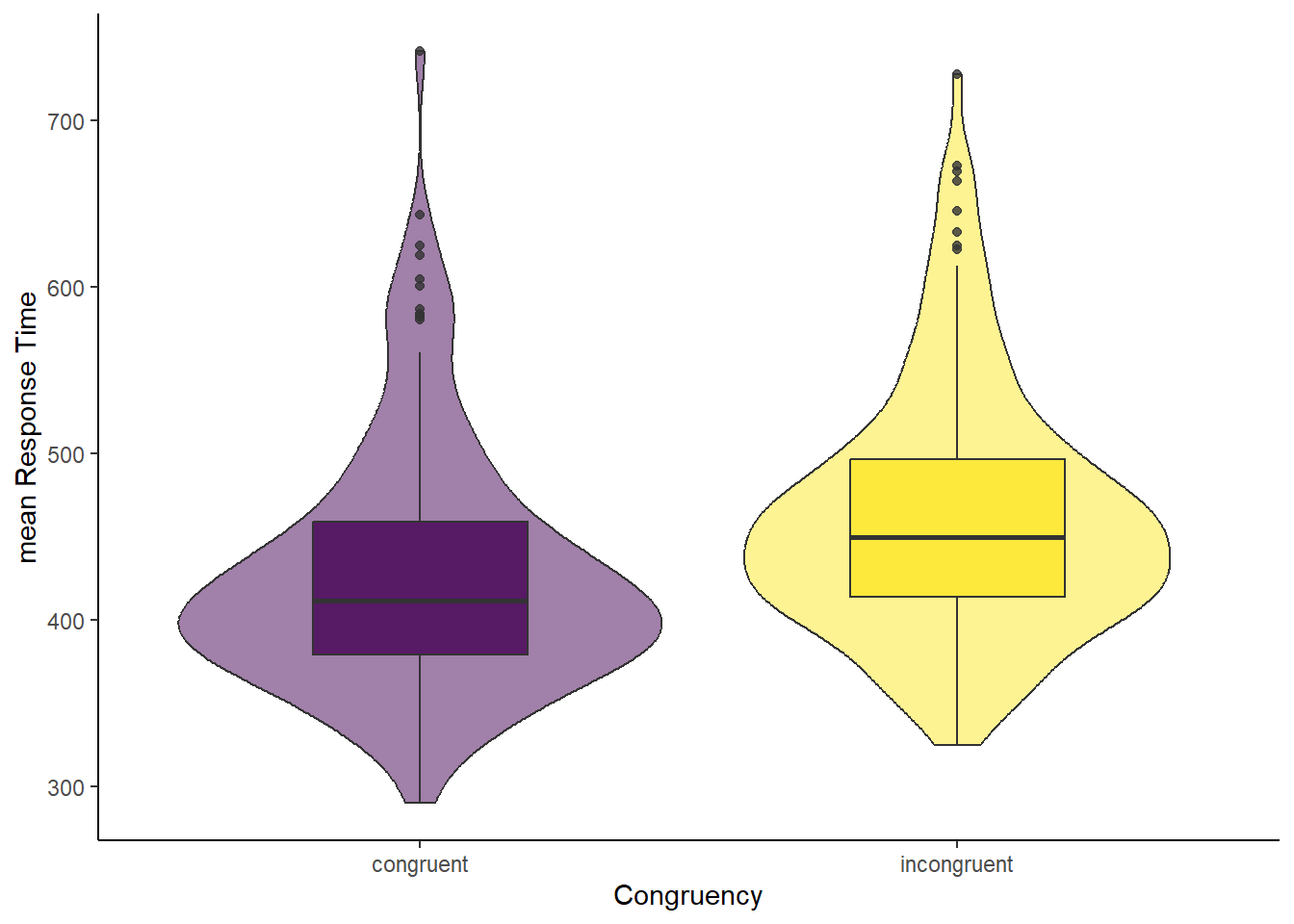
Again, we need to calculate the mean response time (RT) for both congruent and incongruent trials per participant. As we did last week, we can also compute the Simon effect as the difference score between incongruent and congruent trials.

Tip

To keep all the data in one place, we should join this output with the demographics. While you won’t need the demographic information for the t-test itself, having it included will give you a complete dataframe. This can be useful when you need to calculate demographics for the Methods section; for example if you end up excluding data points, you can compute sample size, age, and gender splits straight away rather than having to apply the same exclusion criteria to a different data object.

For the paired version of the t.test, we need the congruent and incongruent trials in separate columns, ensuring each participant still has only one row in the dataframe (i.e., wide format). Below is the output we aim to achieve:

participant gender age education similarity congruent incongruent simon_effect
T1 Female 50 High school same 475.0032 508.2835 33.28029
T10 Male 45 Associate’s degree same 420.1515 401.5800 -18.57148
T109 Male 33 Bachelor’s degree same 339.5343 375.7152 36.18085
T11 Female 71 High school same 516.9722 542.3111 25.33889
T111 Female 34 High school same 373.5778 394.0665 20.48874
Your Turn

Challenge yourself! Try recreating the table without hints this time. (Note: The table above is abbreviated; your data object should include the data from ALL participants.)

simon_effect <- zwaan_data %>% 
  pivot_longer(cols = session1_congruent:session2_incongruent, names_to = "col_headings", values_to = "RT") %>% 
  separate(col_headings, into = c("Session_number", "congruency"), sep = "_") %>% 
  group_by(participant, similarity, congruency) %>% 
  summarise(mean_RT = mean(RT)) %>% 
  ungroup() %>% 
  pivot_wider(names_from = congruency, values_from = mean_RT) %>% 
  mutate(simon_effect = incongruent - congruent) %>% 
  full_join(zwaan_demo, by = join_by(participant == twosubjectnumber)) %>% 
  select(participant, gender = gender_response, age = age_response, education = education_response, similarity:simon_effect)
  1. looked at the hints from the last chapter, since we are working with the exact same dataframe today.
  2. saved the data object from last week as a csv file and read it in here.

8.4 Activity 4: Compute descriptives

We want to compute means and standard deviations for both the congruent and the incongruent trials. Then, we will subtract the mean RT of the congruent trials from the mean RT of the incongruent trials to calculate the average difference score between the two conditions.

descriptives <- simon_effect %>% 
  summarise(mean_congruent = mean(congruent),
            sd_congruent = sd(congruent),
            mean_incongruent = mean(incongruent),
            sd_incongruent = sd(incongruent),
            diff = mean_incongruent - mean_congruent, # diff = mean(simon_effect) would also work
            sd_diff = sd(simon_effect))
mean_congruent sd_congruent mean_incongruent sd_incongruent diff sd_diff
427.6528 74.17418 462.0785 74.69692 34.42571 21.59876
Note

Notice that we did not have to use group_by() here because the data is already in wide format.

8.5 Activity 5: Create an appropriate plot

8.5.1 Option 1: congruent and incongruent trials

To create an appropriate plot, we need the data in long format. This format should include a congruency column containing the labels for congruent and incongruent trials, and a mean_RT column to store the corresponding mean response times. Each participant should now have two rows in the dataset.

participant gender age education similarity simon_effect congruency mean_RT
T1 Female 50 High school same 33.28029 congruent 475.0032
T1 Female 50 High school same 33.28029 incongruent 508.2835
T10 Male 45 Associate’s degree same -18.57148 congruent 420.1515
T10 Male 45 Associate’s degree same -18.57148 incongruent 401.5800
T109 Male 33 Bachelor’s degree same 36.18085 congruent 339.5343
Your Turn

First, wrangle data into long format. The first 5 rows should match the output above. Then, use this table to create an appropriate plot that visualises the differences in mean response times between congruent and incongruent trials.

simon_effect_long <- simon_effect %>% 
  pivot_longer(cols = c(congruent, incongruent), names_to = "congruency", values_to = "mean_RT")
ggplot(simon_effect_long, aes(x = congruency, y = mean_RT, fill = congruency)) +
  geom_violin(alpha = 0.5) +
  geom_boxplot(width = 0.4, alpha = 0.8) +
  scale_fill_viridis_d(guide = "none") +
  theme_classic() +
  labs(x = "Congruency", y = "mean Response Time")

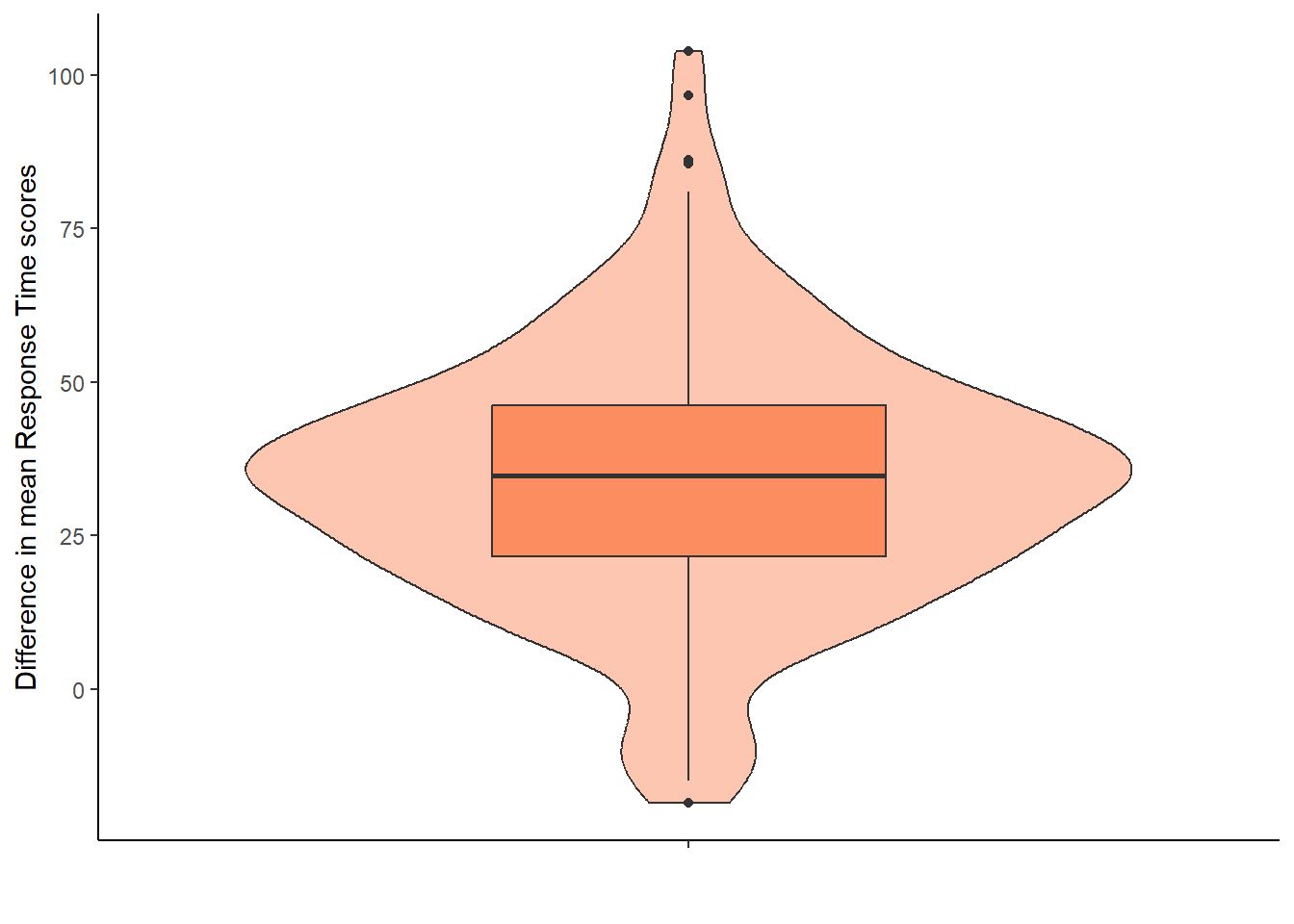
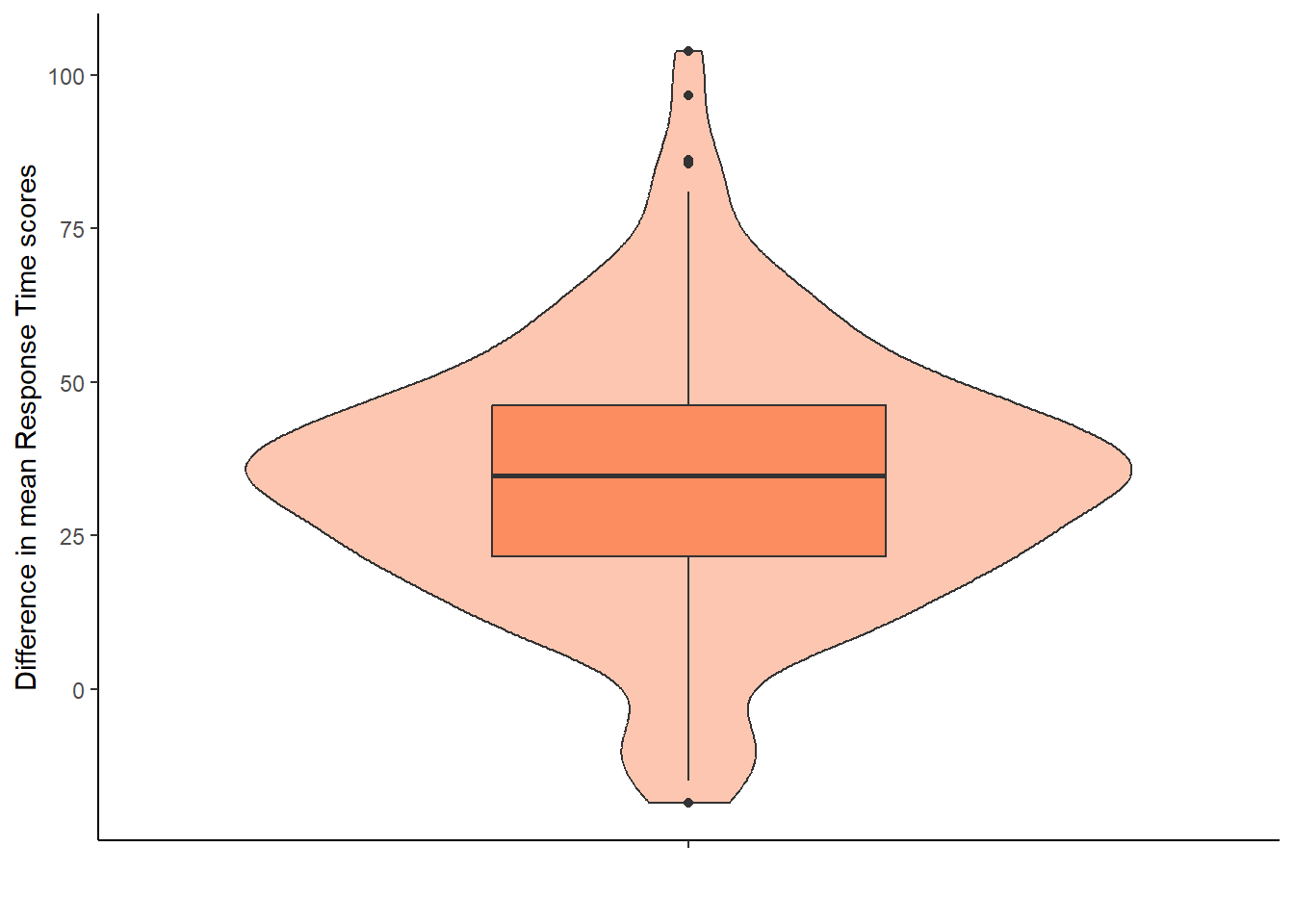
8.5.2 Option 2: difference scores between congruent and incongruent trials

We could have displayed the difference scores between the two conditions directly. This approach would use the simon_effect object without requiring additional data wrangling, as the difference scores are already stored in the simon_effect column.

We want to create a violin-boxplot, but this time it will have only one value on the x-axis instead of a grouping variable as we usually include. This causes the ggplot() function to behave slightly differently. Specifically, you would leave the x-value blank.

ggplot(data, aes(x = "", y = continuous_variable)) +

To add colour, use the usual arguments (e.g., fill, colour), but specify them within the geom_ functions instead of ggplot(), as we typically do.

ggplot(simon_effect, aes(x = "", y = simon_effect)) +
  geom_violin(fill = "#A3319F", alpha = 0.5) +
  geom_boxplot(fill = "#A3319F", width = 0.4) +
  theme_classic() +
  labs(x = "",
       y = "Difference in mean Response Time scores")

8.6 Activity 6: Check assumptions

The assumptions for a paired t-test are fairly similar to the one-sample t-test.

Assumption 1: Continuous DV

The dependent variable needs to be measured at interval or ratio level. We can confirm that by looking at either the columns congruent and incongruent in the object simon_effect. Or the variable mean_RT in simon_effect_long. This assumption holds.

Assumption 2: Data are independent

For a paired t-test this assumption applies to the pair of values, i.e., each pair of values needs to be from a separate participant. We assume this assumption holds for our data.

Assumption 3: Normality

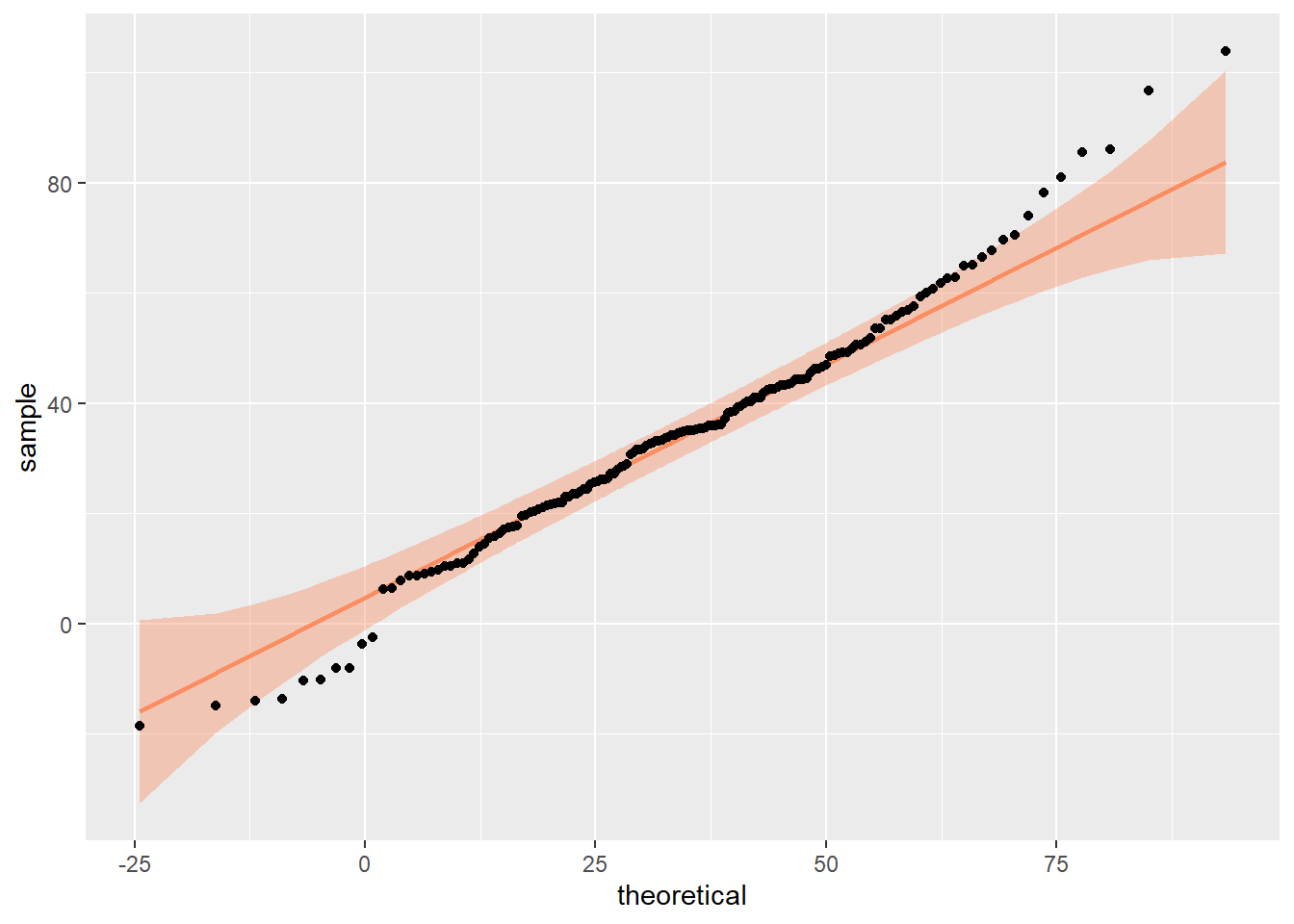
This assumption requires the difference scores to be approximately normally distributed. We cannot see that from the violin-boxplot above (Option 1) and have to plot the difference score, i.e., variable simon_effect.

Your Turn

Plot the difference score.

Think back to the one-sample t-test. How did we plot the normality assumption there?

Explore the three possible approaches in the tabs below.

ggplot(simon_effect, aes(sample = simon_effect)) +
  stat_qq_band(fill = "#FB8D61", alpha = 0.4) +
  stat_qq_line(colour = "#FB8D61") +
  stat_qq_point()

You can use the plot from above if you chose Option 2 in Activity 5, or create a new violin-boxplot if you created plot Option 1 above.

ggplot(simon_effect, aes(x = "", y = simon_effect)) +
  geom_violin(fill = "#FB8D61", alpha = 0.5) + # alpha for opacity, fill for adding colour
  geom_boxplot(fill = "#FB8D61", width = 0.4) + # change width of the boxes
  theme_classic() +
  labs(x = "",
       y = "Difference in mean Response Time scores")

shapiro.test(simon_effect$simon_effect)

    Shapiro-Wilk normality test

data:  simon_effect$simon_effect
W = 0.98588, p-value = 0.1047

Both plots suggest slight deviations from normality in the tails, which are not detected by the Shapiro-Wilk test. However, minor deviations from normality are acceptable for t-tests, especially in the tails of the distribution. Therefore, we conclude that the difference scores are approximately normally distributed.

Note

Assessing normality is never as straightforward as it appears in textbooks. While idealised examples often depict perfectly symmetrical bell curves, real-world data rarely aligns with such precision. Instead, normality exists “on a spectrum”, and it is your responsibility to evaluate whether the data’s shape is sufficiently close to normal for the purposes of your analysis.

This evaluation requires either visual inspection or relying on statistical tests. However, as pointed out in previous chapters, both approaches have limitations and neither provides an absolute answer. Instead of seeking perfection, focus on whether any deviations from normality meaningfully impact the validity of your results.

If any of the assumptions are violated, use the non-parametric equivalent to the paired t-test, see Section 8.10.

8.7 Activity 7: Compute a paired t-test and effect size

We can use the t.test() function again to compute the paired t-test. However, we are stuck with the BaseR pattern data$column once more.

In case you haven’t picked it up by now, I am not much a fan of data$column (i.e., wide format) and prefer the DV ~ IV (i.e., long format) pattern. And there was a time when the t.test() function allowed to add an extra argument paired = TRUE to the formula version but that is no longer the case. 😭😭😭 Now, the argument only works on the default method, specifying arguments x and y separately. And because the default version doesn’t allow us to add a data = argument, we have to revert to data$column.

PS: Carolina disagrees with me and prefers some BaseR every now and then. And that’s totally fine, too - different researchers and coders have their own preferences, which you may have already noticed in the way you code.

Long story short, here are the arguments you need from the data object in wide format (in this case data object simon_effect):

  • data$column for condition 1
  • data$column for condition 2
  • the extra argument paired = TRUE to tell the function we are conducting a paired rather than a two-sample t-test
t.test(simon_effect$congruent, simon_effect$incongruent, paired = TRUE)

    Paired t-test

data:  simon_effect$congruent and simon_effect$incongruent
t = -20.161, df = 159, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -37.79808 -31.05334
sample estimates:
mean difference 
      -34.42571

The output tells us pretty much what we need to know:

  • the test that was conducted (here a paired t-test),
  • the conditions that were compared (here congruent and incongruent),
  • the t-value, degrees of freedom, and a p-value,
  • the alternative hypothesis,
  • a 95% confidence interval,
  • and the mean difference score between both conditions (which also matches with our descriptives above).

The t.test() function does not give us an effect size, so, again, we have to compute it ourselves. We can use the CohensD() function from the lsr package as we did for the one-sample and the two-sample t-test. We can use the formula approach here as well, and add the extra argument method = "paired".

cohensD(simon_effect$congruent, simon_effect$incongruent, method = "paired")
[1] 1.593874
Tip

The cohensD() function would also take a long format formula approach, such as from simon_effect_long, but you would need to make sure that the data within the columns are ordered correctly, i.e., Participant 1: condition 1, condition 2; Participant 2: condition 1, condition 2; etc. If that’s not the case, then your results will be wrong. R helpfully provides a warning message for you to notice and double-check your data accordingly.

cohensD(mean_RT ~ congruency, data = simon_effect_long, method = "paired")
Warning in cohensD(mean_RT ~ congruency, data = simon_effect_long, method =
"paired"): calculating paired samples Cohen's d using formula input. Results
will be incorrect if cases do not appear in the same order for both levels of
the grouping factor
[1] 1.593874

8.8 Activity 8: Sensitivity power analysis

As with the other t-test, we are conducting a sensitivity power analysis to determine the minimum effect size detectable with the number of participants we have in our sample (here n = 160), alpha of 0.05 and power of 0.8. This will tell us if our analysis was sufficiently powered or not.

The function we will use again is pwr.t.test() from the pwr package. The arguments in the formula are the same as for the one-sample t-test; we just need to adjust the number of participants and set the type to “paired”.

pwr.t.test(n = 160, sig.level = 0.05, power = 0.8, type = "paired", alternative = "two.sided")

     Paired t test power calculation 

              n = 160
              d = 0.222858
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number of *pairs*

The minimum effect size we could reliably detect is 0.22. Our actual effect size was 1.59, so this analysis was sufficiently powered. YAY

8.9 Activity 9: The write-up

We hypothesised that there would be a significant difference in the response times between congruent \((M = 427.65 msec, SD = 74.17 msec)\) and incongruent trials \((M = 462.08 msec, SD = 74.70 msec)\) of a Simon task. On average, participants were faster in the congruent compared to the incongruent condition \((M_{diff} = 34.43 msec, SD_{diff} = 21.60 msec)\). Using a within-subjects t-test, the effect was found to be significant and of a large magnitude, \(t(159) = 20.16, p < .001, d = 1.59\). Therefore, we reject the null hypothesis in favour of H1.

8.10 Activity 10: Non-parametric alternative

The Wilcoxon signed-rank test is the non-parametric equivalent to the paired t-test, comparing the difference between the median for two measurements.

Before we compute the test, we need to determine some summary stats (e.g., here we focus on the median scores) for the congruent and incongruent conditions. Similar to the One-sample Wilcoxon signed-rank test, we can use the summary() function again because our data is in wide format.

summary(simon_effect)
 participant           gender               age         education        
 Length:160         Length:160         Min.   :19.00   Length:160        
 Class :character   Class :character   1st Qu.:30.75   Class :character  
 Mode  :character   Mode  :character   Median :37.00   Mode  :character  
                                       Mean   :39.86                     
                                       3rd Qu.:49.00                     
                                       Max.   :71.00                     
  similarity          congruent      incongruent     simon_effect   
 Length:160         Min.   :290.0   Min.   :324.9   Min.   :-18.57  
 Class :character   1st Qu.:379.4   1st Qu.:413.9   1st Qu.: 21.62  
 Mode  :character   Median :411.3   Median :449.7   Median : 34.77  
                    Mean   :427.7   Mean   :462.1   Mean   : 34.43  
                    3rd Qu.:458.7   3rd Qu.:496.3   3rd Qu.: 46.22  
                    Max.   :741.5   Max.   :727.9   Max.   :103.84

Now we can move on to the Wilcoxon signed-rank test. We will use the wilcox.test() function again, but add the argument paired = TRUE.

wilcox.test(simon_effect$congruent, simon_effect$incongruent, paired = TRUE)

    Wilcoxon signed rank test with continuity correction

data:  simon_effect$congruent and simon_effect$incongruent
V = 144, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0
Note

We could have also run a One-sample Wilcoxon signed-rank test on the difference score, but instead of comparing that to a population median (as we did in Section 6.7), we would compare it to 0 to assess whether the median difference between paired observations is significantly different from zero.

wilcox.test(simon_effect$simon_effect, mu = 0)

    Wilcoxon signed rank test with continuity correction

data:  simon_effect$simon_effect
V = 12736, p-value < 2.2e-16
alternative hypothesis: true location is not equal to 0
The V values are different between the 2 approaches - Does that matter?

Yes and no. The order in which you input variables into the function will affect the value of V - has to do with how the ranks are getting assigned. In our column simon_effect we subtracted congruent RT from incongruent RT. To have the exact equivalent, we will need to switch the columns in the wilcox.test() function.

wilcox.test(simon_effect$incongruent, simon_effect$congruent, paired = TRUE)

    Wilcoxon signed rank test with continuity correction

data:  simon_effect$incongruent and simon_effect$congruent
V = 12736, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0

And as you can see, the V values match now.

We should also compute the standardised test statistic Z. Again, we need to calculate Z manually, using the qnorm function on the halved p-value from our Wilcoxon test above.

# storing the p-value
p_wilcoxon <- wilcox.test(simon_effect$incongruent, simon_effect$congruent, paired = TRUE)$p.value

# calculate the z value from half the p-value
z = qnorm(p_wilcoxon/2)
z
[1] -10.72532

To calculate an effect size, we would need to use the function wilcox_effsize() from the rstatix package. Unlike, the wilcox.test() and the t.test() function, wilcox_effsize() expects data to be in long format to be able to use the DV ~ IV pattern. Fortunately, we still have that available in simon_effect_long. We also need to add the argument paired = TRUE.

wilcox_effsize(data = simon_effect_long, formula = mean_RT ~ congruency, paired = TRUE)
.y. group1 group2 effsize n1 n2 magnitude
mean_RT congruent incongruent 0.8479786 160 160 large

Now we have all the numbers to write this up:

A Wilcoxon signed-rank test was conducted to determine whether there was a significant difference in response times between congruent \((Mdn = 411.3 msec)\) and incongruent trials \((Mdn = 449.7 msec)\) in a Simon task. Median response times of Congruent trials were significantly faster \((Mdn = 34.77 msec)\) than incongruent trials, \(Z = -10.73, p < .001, r = .848\). The difference can be classified as large according to Cohen (1992). Therefore, we reject the null hypothesis in favour of H1.

Pair-coding

Important

This week’s pair-coding activity mirrors the one from Chapter 7. While there is no lab scheduled this week, I wanted to provide an opportunity for you to practice. You can treat this either as a “Challenge Yourself” activity or get together with friends to work through it together.

Task 1: Open the R project for the lab

Task 2: Create a new .Rmd file

… and name it something useful. If you need help, have a look at Section 1.3.

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding.

We are using the packages rstatix, tidyverse, qqplotr, lsr today. Make sure to load rstatix in before tidyverse.

We also need to read in dog_data_clean_wide.csv. Again, I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

For the plot, we will need the data in long format. We can either read in dog_data_clean_long.csv to take a shortcut, or wrangle the data from dog_data_wide. I’ve taken the shortcut and named my data object dog_data_long.

Task 4: Tidy data for a paired t-test

Not much tidying to do for today.

Pick a variable of interest and select the pre- and post-scores, and calculate the difference score. Store them in a separate data object with a meaningful name.

I will use Loneliness as an example and call my data object dog_lonely. Regardless of your chosen variable, your data object should look like/ similar to the table below.

RID Loneliness_pre Loneliness_post Loneliness_diff
1 2.25 1.70 -0.55
2 1.90 1.60 -0.30
3 2.25 2.25 0.00
4 1.75 2.05 0.30
5 2.85 2.70 -0.15

In dog_data_long, we want to turn Stage into a factor so we can re-order the labels (i.e., “pre” before “post”).

## Task 3
library(rstatix)
library(tidyverse)
library(lsr)

dog_data_wide <- read_csv("data/dog_data_clean_wide.csv")
Rows: 284 Columns: 24
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (3): GroupAssignment, Year_of_Study, Live_Pets
dbl (21): RID, Age_Yrs, Consumer_BARK, Flourishing_pre, Flourishing_post, PA...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
dog_data_long <- read_csv("data/dog_data_clean_long.csv")
Rows: 568 Columns: 16
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (4): GroupAssignment, Year_of_Study, Live_Pets, Stage
dbl (12): RID, Age_Yrs, Consumer_BARK, Flourishing, PANAS_PA, PANAS_NA, SHS,...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## Task 4
dog_lonely <- dog_data_wide %>% 
  select(RID, Loneliness_pre, Loneliness_post) %>% 
  mutate(Loneliness_diff = Loneliness_post - Loneliness_pre)

dog_data_long <- dog_data_long %>% 
  mutate(Stage = factor(Stage,
                        levels = c("pre", "post")))

Task 5: Compute descriptives

We want to determine the mean and sd of:

  • the pre-scores
  • the post-scores, and
  • the difference scores

Store them in a data object called descriptives.

descriptives <- dog_lonely %>% 
  summarise(mean_pre = mean(Loneliness_pre),
            sd_pre = sd(Loneliness_pre),
            mean_post = mean(Loneliness_post),
            sd_post = sd(Loneliness_post),
            diff = mean(Loneliness_diff),
            sd_diff = sd(Loneliness_diff))

Task 6: Check assumptions

Assumption 1: Continuous DV

Is the dependent variable (DV) continuous? Answer:

Assumption 2: Data are independent

Each pair of values in the dataset has to be independent, meaning each pair of values needs to be from a separate participant. Answer:

Assumption 3: Normality

Looking at the violin-boxplots below, do you think the assumption of normality holds?

Note

The labels of Plot 2 turned out to be quite long here. I’ve used the escape character \n here. to break up the title across 2 lines.

## Plot 1
ggplot(dog_data_long, aes(x = Stage, y = Loneliness, fill = Stage)) +
  geom_violin(alpha = 0.5) +
  geom_boxplot(width = 0.4, alpha = 0.8) +
  scale_fill_viridis_d(guide = "none") +
  theme_classic() +
  labs(x = "Time point", y = "mean Loneliness Scores")

## Plot 2
ggplot(dog_lonely, aes(x = "", y = Loneliness_diff)) +
  geom_violin(fill = "#21908C", alpha = 0.5) +
  geom_boxplot(fill = "#21908C", width = 0.4) +
  theme_classic() +
  labs(x = "",
       y = "Difference in mean Loneliness scores \nbetween pre- and post- intervention") # \n forces a manual line break in the axis label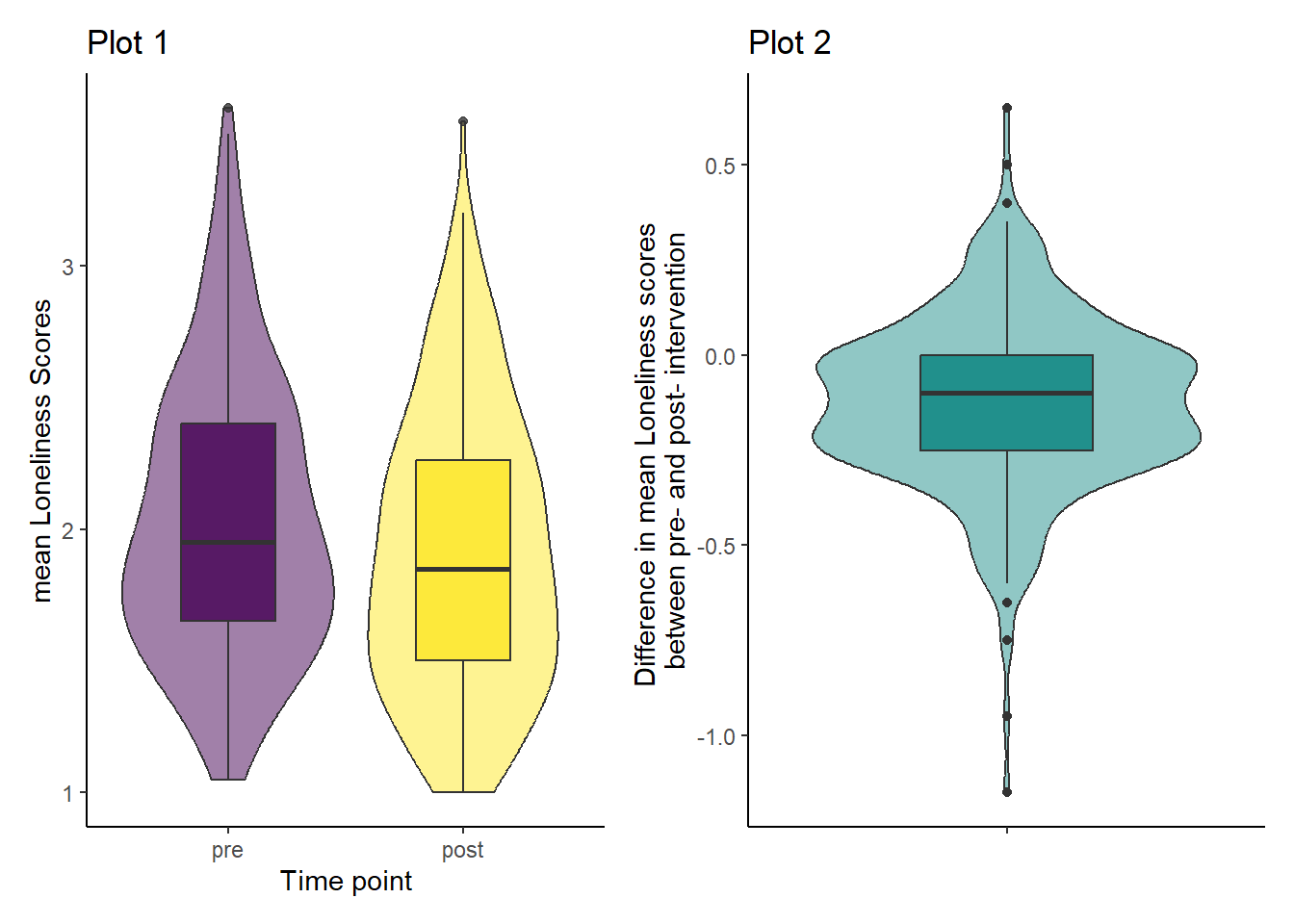

Plots displayed to assess normality assumption

Answer:

Conclusion from assumption tests

With all assumptions tested, which statistical test would you recommend for this analysis?

Answer:

Task 7: Computing a paired-sample t-test with effect size & interpret the output

  • Step 1: Compute the paired-sample t-test. The structure of the function is as follows:
t.test(your_data$var1, your_data$var2, paired = TRUE)
t.test(dog_lonely$Loneliness_pre, dog_lonely$Loneliness_post, paired = TRUE)
  • Step 2: Calculate an effect size

Calculate Cohen’s D. The structure of the function is as follows:

cohensD(your_data$var1, your_data$var2, method = "paired")
cohensD(dog_lonely$Loneliness_pre, dog_lonely$Loneliness_post, method = "paired")
  • Step 3: Interpreting the output

Below are the outputs for the descriptive statistics (table), paired-samples t-test (main output), and Cohen’s D (last line starting with [1]). Based on these, write up the results in APA style and provide an interpretation.

mean_pre sd_pre mean_post sd_post diff sd_diff
2.040187 0.5304488 1.914298 0.5344914 -0.1258895 0.2290269 

    Paired t-test

data:  dog_lonely$Loneliness_pre and dog_lonely$Loneliness_post
t = 9.2632, df = 283, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.09913876 0.15264034
sample estimates:
mean difference 
      0.1258895 

[1] 0.5496716

We hypothesised that there would be a significant difference between Loneliness measured before (M = , SD = ) and after (M = , SD = ) the dog intervention. On average, participants felt less lonely after the intervention (M{diff} = , SD{diff} = ). Using a paired-samples t-test, the effect was found to be and of a magnitude, t() = , p , d = . We therefore .

Test your knowledge

Question 1

What is the main purpose of an paired-samples t-test?

The paired t-test is used when comparing means from related groups. It requires two measurements from the same group or individual. Examples could be before-and-after measurements (e.g., pre- and post-intervention), or repeated measures (e.g., exercise under 2 different conditions, such as indoor and outdoor), etc.

Question 2

Which of the following is a key assumption of the paired t-test?

The paired t-test assumes that the differences between the paired observations are normally distributed, as the test is applied to these differences, not the raw scores.

Question 3

What is the null hypothesis for a paired t-test?

The paired t-test specifically tests whether the mean difference between paired observations (e.g., pre-test and post-test scores) is zero, indicating no systematic difference.

Why the other options are incorrect:

  • The means of two independent groups are equal: This describes the null hypothesis for an independent t-test, not a paired t-test. The paired t-test is used for related groups or repeated measures, not independent groups.
  • The variances of the two samples are equal: This is an assumption that applies to the independent t-test, which compares two unrelated groups. The paired t-test does not test variances; it focuses on the differences between paired observations.
  • There is no relationship between two variables: This is not the null hypothesis for a paired t-test. It relates more to correlation or regression analyses, which assess relationships between variables, not mean differences.

Question 4

A paired-samples t-test was conducted to compare sleep quality scores with (M = 7.5, SD = 1.8) and without (M = 6.0, SD = 1.9) white noise, t(29) = 4.55, p < .001, d = 0.82. Answer the questions below.

  • How many participants were included in the study?
  • What is the effect size, and how would you describe its magnitude? The effect size is and of magnitude.
  • Is the result statistically significant?
  • Based on the means and standard deviations, how would you summarise the direction of the effect?

The degrees of freedom for a paired-samples t-test are calculated as N - 1 for the number of paired observations. With df = 29, the sample size is 30 participants.

An effect size of d = 0.82 is considered large. This suggests a meaningful and substantial difference in sleep quality between the two conditions.

The result is statistically significant. The p-value (p < .001) indicates that the observed difference in the sample is very unlikely to occur if we assume there is no true difference in the population.

The mean sleep quality score with white noise (M = 7.5) is higher than without white noise (M = 6.0), indicating improved sleep quality with white noise.