7  Two-sample t-test

Intended Learning Outcomes

In this chapter, we will focus on two-sample t-tests, also known as between-groups, between-subjects, or independent-samples t-tests. By the end of this chapter, you should be able to:

  • Compute a two-sample t-test and effectively report the results.
  • Understand when to use a non-parametric equivalent of the two-sample t-test, compute it, and report the results.

Individual Walkthrough

7.1 Activity 1: Setup & download the data

This week, we will be working with a new dataset. Follow the steps below to set up your project:

  • Create a new project and name it something meaningful (e.g., “2A_chapter7”, or “07_independent_ttest”). See Section 1.2 if you need some guidance.
  • Create a new .Rmd file and save it to your project folder. See Section 1.3 if you get stuck.
  • Delete everything after the setup code chunk (e.g., line 12 and below)
  • Download the reduced version of a new dataset here: data_ch7.zip. The zip folder includes the following files:
    • CodebookSimonTask.xlsx: A codebook with detailed variable descriptions
    • DemoSimonTask.csv: A CSV file containing demographic information
    • MeanSimonTask.csv: A CSV file with the mean response times
    • Sup_Mats_Simon_Task.docx: A Word document with Supplementary Materials providing additional details about the task
    • RawDataSimonTask.csv: The raw data file, allowing you to explore what experimental data looks like prior to pre-processing.
  • Extract the data files from the zip folder and place them in your project folder. If you need help, see Section 1.4.

Citation

Zwaan, R. A., Pecher, D., Paolacci, G., Bouwmeester, S., Verkoeijen, P., Dijkstra, K., & Zeelenberg, R. (2018). Participant nonnaiveté and the reproducibility of cognitive psychology. Psychonomic Bulletin & Review, 25, 1968-1972. https://doi.org/10.3758/s13423-017-1348-y

The data and supplementary materials are available on OSF: https://osf.io/ghv6m/

Abstract

Many argue that there is a reproducibility crisis in psychology. We investigated nine well-known effects from the cognitive psychology literature—three each from the domains of perception/action, memory, and language, respectively—and found that they are highly reproducible. Not only can they be reproduced in online environments, but they also can be reproduced with nonnaïve participants with no reduction of effect size. Apparently, some cognitive tasks are so constraining that they encapsulate behavior from external influences, such as testing situation and prior recent experience with the experiment to yield highly robust effects.

Changes made to the dataset

  • The dataset, demographic information, and Supplementary Materials have been reduced to include only information related to the Simon Task. The full dataset, which includes the other eight tasks, is available on OSF.
  • No other changes were made.

7.2 Activity 2: Library and data for today

Today, we’ll be using the following packages: rstatix, tidyverse, car, lsr, and pwr. You may need to install the packages before using them Make sure that rstatix is loaded in before tidyverse to avoid masking certain functions that we will need later.

We will also read in the data from MeansSimonTask.csv and the demographic information from DemoSimonTask.csv.

# load in the packages
???

# read in the data
zwaan_data <- ???
zwaan_demo <- ???
# load in the packages
library(rstatix)
library(tidyverse)
library(car)
library(lsr)
library(pwr)

# read in the data
zwaan_data <- read_csv("MeansSimonTask.csv")
zwaan_demo <- read_csv("DemoSimonTask.csv")

7.3 Activity 3: Familiarise yourself with the data

As usual, take some time to familiarise yourself with the data before starting on the between-subjects t-test. Also, more importantly, have a look at the Supplementary Materials in which the Simon effect is explained in more depth.

In general, the Simon effect refers to the phenomenon where participants respond faster when the stimulus appears on the same side of the screen as the button they need to press (i.e., a congruent condition). Conversely, response times are slower when the stimulus appears on the opposite side of the screen from the required button (i.e., an incongruent condition).

In this experiment, all participants completed two sessions of trials. However, they were divided into two groups based on the stimuli they received:

  • Same Stimuli Group: Half of the participants received the same set of stimuli in both sessions.
  • Different Stimuli Group: The other half received a different set of stimuli in session 2 compared to session 1.

7.3.1 Potential research questions and hypotheses

  • Potential research question: “Is there a significant difference in the Simon effect between participants who received the same stimuli in both sessions compared to those who received different stimuli?”
  • Null Hypothesis (H0): “There is no significant difference in the Simon effect between participants who received the same stimuli in both sessions and those who received different stimuli.”
  • Alternative Hypothesis (H1): “There is a significant difference in the Simon effect between participants who received the same stimuli in both sessions and those who received different stimuli.”

7.4 Activity 4: Preparing the dataframe

The data is already in a very good shape, however, we need to perform some data wrangling to compute the Simon effect.

Steps to calculate the Simon effect:

  1. For each participant, compute the mean response time (RT) for congruent trials and the mean RT for incongruent trials
  2. Subtract the mean RT of congruent trials from the mean RT of incongruent trials to calculate the Simon effect

To streamline analysis, we should join this output with the demographics data to have all relevant information in one place.

Basically, we want to create a tibble that has the following content. [Note that I re-arranged the columns and re-labelled some of them in a final step, so your column names and/or order might be slightly different, but content should match.]

participant gender age education similarity congruent incongruent simon_effect
T1 Female 50 High school same 475.0032 508.2835 33.28029
T10 Male 45 Associate’s degree same 420.1515 401.5800 -18.57148
T109 Male 33 Bachelor’s degree same 339.5343 375.7152 36.18085
T11 Female 71 High school same 516.9722 542.3111 25.33889
T111 Female 34 High school same 373.5778 394.0665 20.48874

Obviously, there are various ways to achieve this, so feel free to explore and come up with your own approach. However, we will provide step-by-step instructions for one of those ways that will get you the desired output.

  • Step 1: Convert the data from wide format to long format, so that all RT values are consolidated into a single column. This transformation will result in each participant having four rows.
  • Step 2: There should be a column now that contained the previous column headings with information on session number and congruency. Separate this information into 2 separate columns (i.e., session number and congruency).
  • Step 3: Compute the mean RT values for each combination of participant, similarity, and congruency
  • Step 4: Pivot the data back to wide format so that the mean RT values for congruent and incongruent trials are placed in two separate columns.
  • Step 5: Add a new column called the simon_effect that calculates the Simon effect by subtracting the mean RT for congruent trials from the mean RT for incongruent trials.
  • Step 6: Merge this processed dataset with the demographics data to ensure all relevant information is in one table.
  • Step 7: Feel free to rearrange the order of columns and/or rename them to match your output with ours (not strictly necessary tbh)
simon_effect <- zwaan_data %>% 
  pivot_longer(cols = session1_congruent:session2_incongruent, names_to = "col_headings", values_to = "RT") %>% 
  separate(col_headings, into = c("Session_number", "congruency"), sep = "_") %>% 
  group_by(participant, similarity, congruency) %>% 
  summarise(mean_RT = mean(RT)) %>% 
  ungroup() %>% 
  pivot_wider(names_from = congruency, values_from = mean_RT) %>% 
  mutate(simon_effect = incongruent - congruent) %>% 
  full_join(zwaan_demo, by = join_by(participant == twosubjectnumber)) %>% 
  select(participant, gender = gender_response, age = age_response, education = education_response, similarity:simon_effect)

7.5 Activity 5: Compute descriptives

Next, we want to compute number of participants (n), means and standard deviations for each group (i.e., same and different) of our variable of interest (i.e., simon_effect).

descriptives <- simon_effect %>% 
  group_by(similarity) %>% 
  summarise(n = n(),
            mean_RT = mean(simon_effect),
            sd_RT = sd(simon_effect)) %>% 
  ungroup()

descriptives
similarity n mean_RT sd_RT
different 80 32.85726 20.79313
same 80 35.99415 22.39601

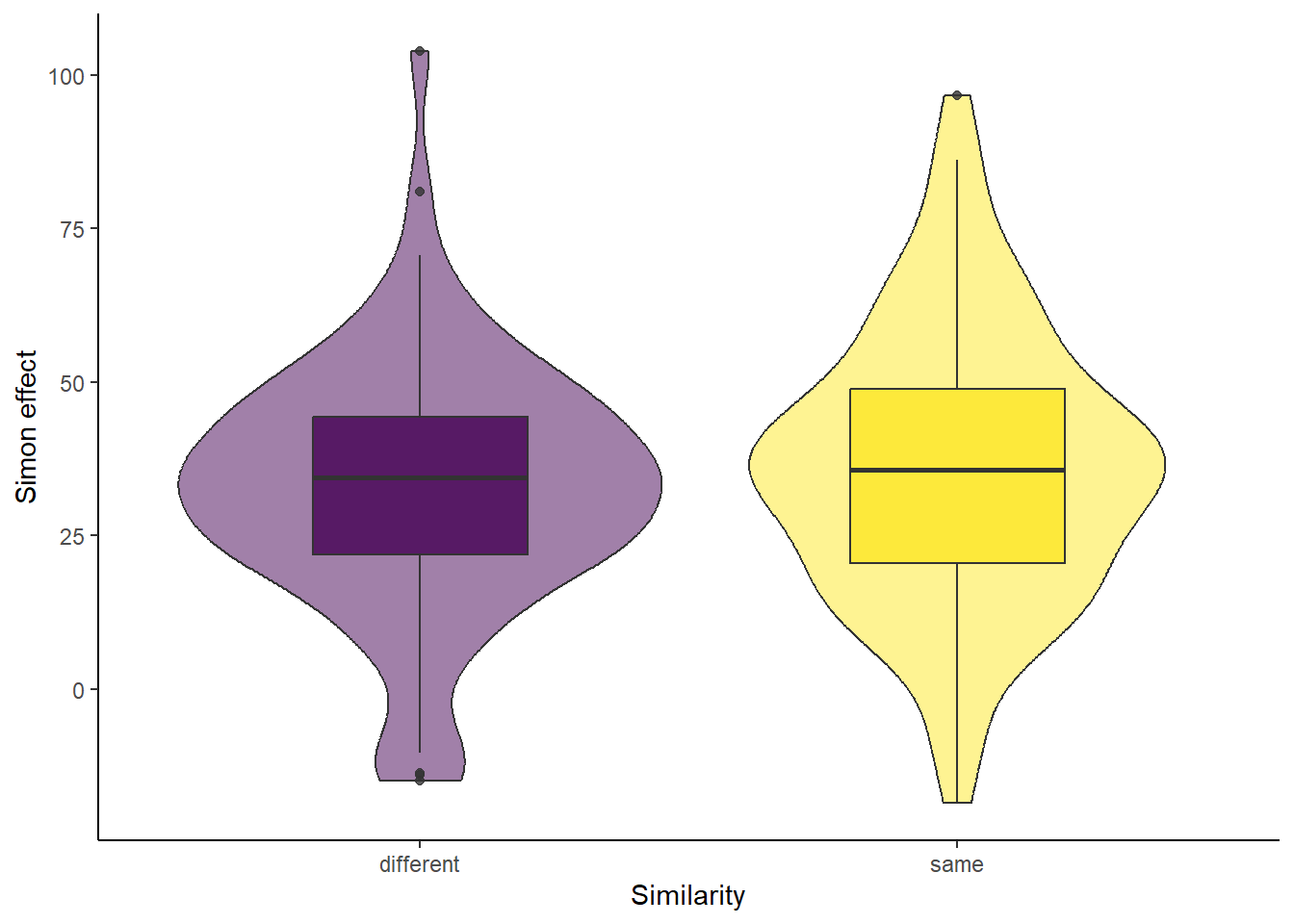
7.6 Activity 6: Create an appropriate plot

Which plot would you choose to represent the data appropriately? Create a plot that effectively visualises the data, and then compare it with the solution provided below.

ggplot(simon_effect, aes(x = similarity, y = simon_effect, fill = similarity)) +
  geom_violin(alpha = 0.5) +
  geom_boxplot(width = 0.4, alpha = 0.8) +
  scale_fill_viridis_d(guide = "none") +
  theme_classic() +
  labs(x = "Similarity", y = "Simon effect")

7.7 Activity 7: Check assumptions

Assumption 1: Continuous DV

The dependent variable must be measured at interval or ratio level. We can confirm that by looking at simon_effect.

Assumption 2: Data are independent

There should be no relationship between the observations. Scores in one condition or observation should not influence scores in another. We assume this assumption holds for our data.

Assumption 3: Homoscedasticity (homogeneity of variance)

This assumption requires the variances between the two groups to be similar (i.e., homoscedasticity). If the variances between the 2 groups are dissimilar/unequal, we have heteroscedasticity.

We can test this using a Levene’s Test for Equality of Variance which is available in the package car. The first argument specifies the formula in the format DV ~ IV. Here:

  • The dependent variable (DV) is simon_effect (continuous)
  • The independent variable (IV) is similarity (the grouping variable)

To perform the test, separate the variables with a tilde (~), and specify the dataset using the data argument:

leveneTest(simon_effect ~ similarity, data = simon_effect)
Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.
Df F value Pr(>F)
group 1 0.7263221 0.3953679
158 NA NA

The warning message tells us that the grouping variable was converted into a factor. Oops, I guess we forgot to convert similarity into a factor during data wrangling.

The test output shows a p-value greater than .05. This indicates that we do not have enough evidence to reject the null hypothesis. Therefore, the variances across the two groups can be assumed equal.

You would report this result in APA style: A Levene’s test of homogeneity of variances was used to compare the variances of the same and the different groups. The test indicated that the variances were homogeneous, \(F(1,158) = 0.73, p = .395\).

Important

The t-test we are conducting is a Welch t-test by default. The Welch t-test provides similar results to a Student’s t-test when variances are equal but is preferred when variances are unequal.

This means that even if Levene’s test returns a significant p-value, indicating that the variances between the groups are unequal, the Welch t-test remains appropriate and valid for analysis.

Assumption 4: DV should be approximately normally distributed

It’s important to note that this assumption requires the dependent variable to be normally distributed within each group.

We can either use our eyeballs again on the violin-boxplot we created earlier (or use a qqplot, density plot, or histogram instead), OR compute a statistic like the Shapiro-Wilk’s test we already mentioned previously for the one-sample t-test. However, keep in mind that with large sample sizes (approximately 80 participants per group), this test may flag minor deviations from normality as significant, even if the data is reasonably normal.

Visual inspection suggests that both groups are approximately normally distributed. The “same” group appears slightly more normally distributed than the “different” group, which has a small peak in the lower tail. Despite this, both distributions seem normal enough for practical purposes with real-world data.

Tip: Visual inspection

If you want to use a histogram, density plot or qqplot (the ones created with the ggplot2 and qqplotr packages), you can simply add a facet_wrap() function to display the plots separately for each group.

If you are using the Q-Q plot function from the car package, you will need to create separate data objects filtered for each group before generating Q-Q plots for the groups individually.

Task: Compute Shapiro-Wilk’s test

As mentioned above, the function for the Shapiro-Wilk’s test does not allow for a formula. This means you will need to create separate data objects for the two groups first. Consider this a good opportunity to practice using the filter() function.

Step-by-step instructions:

  1. Create separate data objects for the same and different groups.
  2. Run the Shapiro-Wilk test on each group’s data.
  3. Examine the results. What do you conclude from the test outcomes?
## same group
same <- simon_effect %>% 
  filter(similarity == "same")

shapiro.test(same$simon_effect)

## different group
different <- simon_effect %>% 
  filter(similarity == "different")

shapiro.test(different$simon_effect)

    Shapiro-Wilk normality test

data:  same$simon_effect
W = 0.98921, p-value = 0.7447


    Shapiro-Wilk normality test

data:  different$simon_effect
W = 0.96949, p-value = 0.05262

Interpretation:

Shapiro-Wilk’s test also suggests that the data for both groups, “same” and “different”, are normally distributed as all p-values are above .05.

Again, if you used this method in your report, you would have to write up the results in APA style (refer to the section on the one-sample t-test for guidance on reporting).

Important

If you have read the Delacre et al. (2017) paper (https://rips-irsp.com/articles/10.5334/irsp.82), you might be aware that the normality assumption is not critical for the Welch t-test.

This means that, whether you consider both groups to be “normally distributed” or interpret one as slightly deviating from normality, the Welch t-test remains an appropriate choice for this dataset.

After verifying all the assumptions, we concluded that they were met. Therefore, we will compute a Welch two-sample t-test.

7.8 Activity 8: Compute a Two-sample t-test and effect size

The t.test() function, which we previously used for the one-sample t-test, can also be used here, but with a slightly different approach. It supports a formula option, which simplifies the process. This means we don’t need to wrangle the data further or use the $ operator to access columns directly. Instead, we can specify the formula as DV ~ IV.

The key arguments for t.test() are:

  • The first argument in the formula with the pattern DV ~ IV
  • The second argument is the data
  • The third argument is specifying whether variances are equal between the groups. The default value is var.equal = FALSE, which conducts a Welch t-test. If you set var.equal = TRUE, you would conduct a Student t-test instead.
  • The 4th argument alternative specifies the alternative hypothesis. The default value is “two.sided”, meaning the test will check for differences in both directions (i.e., a non-directional hypothesis)
t.test(simon_effect ~ similarity, data = simon_effect, var.equal = FALSE, alternative = "two.sided")

    Welch Two Sample t-test

data:  simon_effect by similarity
t = -0.91809, df = 157.14, p-value = 0.36
alternative hypothesis: true difference in means between group different and group same is not equal to 0
95 percent confidence interval:
 -9.885574  3.611799
sample estimates:
mean in group different      mean in group same 
               32.85726                35.99415

The output of the t.test() function tells us:

  • the type of test that was conducted (here Welch t-test)
  • the variables that were tested (here simon_effect by similarity),
  • the t-value, degrees of freedom, and p,
  • the alternative hypothesis tested,
  • a 95% confidence interval for the difference between group means, and
  • the mean of both groups (which should match our descriptive stats)

The t.test() function does not calculate an effect size, so we have to compute it separately once again. As with the one-sample t-test, we can use the CohensD() function from the lsr package. The formula-based approach works here too. For the Welch version of the t-test, you need to include the argument method = "unequal" in the CohensD() function to account for unequal variances.

cohensD(simon_effect ~ similarity, data = simon_effect, method = "unequal")
[1] 0.1451628

7.9 Activity 9: Sensitivity power analysis

Next, we will conduct a sensitivity power analysis to determine the minimum effect size that could have been reliably detected with our sample size, an alpha level of 0.05, and a power of 0.8.

To perform this analysis, we use the pwr.t.test() from the pwr package. The arguments are the same as those used for the one-sample t-test, but with a few adjustments:

  • Number of Participants: Specify the number of observations per sample (i.e., n)
  • Test Type: Set the type argument to “two.sample” for a two-sample t-test.
pwr.t.test(n = 80, sig.level = 0.05, power = 0.8, type = "two.sample", alternative = "two.sided")

     Two-sample t test power calculation 

              n = 80
              d = 0.445672
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

Sooo, the smallest effect size we can detect with a sample size of 80 participants in each group, an alpha level of .05, and power of .8 is 0.45. This is larger than the actual effect size we calculated using the CohensD() function (i.e., 0.14). This indicates that our analysis is underpowered to detect such a small effect size.

Hypothetical Replication Study

Out of curiosity, if we were to replicate this study and wanted to reliably detect an effect size as small as 0.14, how many participants would we need?

We can use the pwr.t.test() function again. This time, instead of specifying n, we provide the effect size (d = 0.14). The result shows that we would need approximately 1,500 participants in total (750 per group). Ooft; that’s quite a few people to recruit.

However, it’s worth noting that an effect size of 0.14 may not be practically meaningful, even if statistically detectable.

pwr.t.test(d = 0.145, sig.level = 0.05, power = 0.8, type = "two.sample", alternative = "two.sided")

     Two-sample t test power calculation 

              n = 747.5833
              d = 0.145
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group
But my two groups have unequal sample sizes, and there is only one n in pwr.t.test. What do I do?

No problem! You can use the pwr.t2n.test() function, which allows you to specify different sample sizes for the two groups (n1 and n2).

The rest of the arguments are essentially the same as with pwr.t.test(). Additionally, there is no need to specify the type argument, as the function is specifically designed for two-sample t-tests with unequal sample sizes.

pwr.t2n.test(n1 = NULL, n2= NULL, d = NULL, sig.level = 0.05, power = NULL, alternative = c("two.sided", "less","greater"))

Let’s try it for our example. We should get the same result though.

pwr.t2n.test(n1 = 80, n2= 80, sig.level = 0.05, power = 0.8, alternative = "two.sided")

     t test power calculation 

             n1 = 80
             n2 = 80
              d = 0.445672
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

7.10 Activity 10: The write-up

We hypothesised that there would be a significant difference in the Simon effect between participants who received the same stimuli in both sessions \((N = 80, M = 35.99 msec, SD = 22.40 msec)\) and those who received different stimuli \((N = 80, M = 32.86 msec, SD = 20.79 msec)\). Using a Welch two-sample t-test, the effect was found to be non-significant and of a small magnitude, \(t(157.14) = 0.92, p = .360, d = 0.15\). The overall mean difference between groups was small \((M_{diff} = 3.14 msec)\). Therefore, we fail to reject the null hypothesis.

7.11 Activity 11: Non-parametric alternative

The Mann-Whitney U-test is the non-parametric equivalent of the independent two-sample t-test. It is used to compare the medians of two samples and is particularly useful when the assumptions of the t-test are not met.

According to Delacre et al. (2017), the Mann-Whitney U-test is robust to violations of normality but remains sensitive to heteroscedasticity. In this case, we don’t need to worry about heteroscedasticity, as the variances in the two groups are equal. However, it’s important to keep this in mind when assessing assumptions and interpreting results with other datasets.

First, let’s start by computing some summary statistics for each group.

simon_effect %>% 
  group_by(similarity) %>% 
  summarise(n = n(), 
            median = median(simon_effect))
similarity n median
different 80 34.44134
same 80 35.68470

To conduct a Mann-Whitney U-test, use the wilcox.test() function. As with the independent t-test, you can use the formula approach DV ~ IV. The code structure is identical to what we used for the independent t-test.

wilcox.test(simon_effect ~ similarity, data = simon_effect)

    Wilcoxon rank sum test with continuity correction

data:  simon_effect by similarity
W = 3001, p-value = 0.4981
alternative hypothesis: true location shift is not equal to 0

We should compute the standardised test statistic Z manually. To do this, use the qnorm() function on the halved p-value obtained from the Wilcoxon test conducted earlier.

# storing the p-value
p_wilcoxon <- wilcox.test(simon_effect ~ similarity, data = simon_effect)$p.value

# calculate the z value from half the p-value
z = qnorm(p_wilcoxon/2)
z
[1] -0.6774047

The effect size for the Mann-Whitney U-test is r. To compute r, we’d need the standardised test statistic z and divide that the square-root of the number of pairs n: \(r = \frac{|z|}{\sqrt n}\).

Alternatively, you can use the wilcox_effsize() function from the rstatix package to simplify the process.

The arguments for this function are slightly different in order but otherwise identical to those used in the wilcox.test() function above.

wilcox_effsize(data = simon_effect, formula = simon_effect ~ similarity)
.y. group1 group2 effsize n1 n2 magnitude
simon_effect different same 0.0536884 80 80 small

This is once again considered a small effect. Anyway, we do have all the numbers now to write up the results:

A Mann-Whitney U-test was conducted to determine whether there was a significant difference in the Simon effect between participants who received the same stimuli in both sessions \((N = 80, Mdn = 35.68 \text{msec})\) and those who received different stimuli \((N = 80, Mdn = 34.44 \text{msec})\). The results indicate that the median difference in response time was non-significant and of small magnitude, \(W = 3001, Z = -0.68, p = .498, r = .054\). Therefore, we fail to reject the null hypothesis.

Pair-coding

Task 1: Open the R project for the lab

Task 2: Create a new .Rmd file

… and name it something useful. If you need help, have a look at Section 1.3.

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding.

We are using the packages tidyverse, car, and lsr today, and the data file we need to read in is dog_data_clean_wide.csv. I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

If you have not worked through chapter 7 yet, you may need to install a few packages first before you can load them into the library, for example, if car is missing, run install.packages("car") in your CONSOLE.

Task 4: Tidy data for a two-sample t-test

For today’s task, we want to analyse how students’ psychological well-being scores differed at the post_intervention time point. Specifically, we will compare the scores of students who directly interacted with the dogs (Group direct)to those who only talked to the dog handlers (Group control).

To achieve that, we need to select all relevant columns from dog_data_wide, and narrow down the dataframe to only include students assigned either to the direct or the control groups.

  • Step 1: Select all relevant columns from dog_data_wide. For the task at hand, those would be the participant ID RID, GroupAssignment, and Flourishing_post. Store this data in an object called dog_independent.

  • Step 2: Narrow down dog_independent to only include GroupAssignment groups direct or the control.

  • Step 3: Convert GroupAssignment into a factor.

dog_independent <- ??? %>% 
  # Step 1
  select(???, ???, ???) %>% 
  # Step 2
  filter(??? %in% c(???, ???)) %>% 
  # Step 3
  mutate(GroupAssignment = ???())
# loading tidyverse and lsr into the library
library(tidyverse)
library(car)
library(lsr)

# reading in `dog_data_clean_wide.csv`
dog_data_wide <- read_csv("dog_data_clean_wide.csv")

# Task 4: Tidying 
dog_independent <- dog_data_wide %>% 
  # Step 1
  select(RID, GroupAssignment, Flourishing_post) %>% 
  # Step 2
  filter(GroupAssignment %in% c("Control", "Direct")) %>% 
  # Step 3
  mutate(GroupAssignment = factor(GroupAssignment))

Task 5: Compute descriptives

Calculate the sample size (n), the mean, and the standard deviation of the psychological well-being score for both groups. Save the output in an object called dog_independent_descriptives. The resulting dataframe should look like this:

GroupAssignment n mean_Flourishing sd_Flourishing
Control 94 5.718085 0.7709738
Direct 95 5.776316 0.8638912 
dog_independent_descriptives <- dog_independent %>% 
  group_by(???) %>% 
  summarise(n = n(),
            mean_Flourishing = mean(???),
            sd_Flourishing = sd(???)) %>% 
  ungroup()
# Task 5: Means & SD
dog_independent_descriptives <- dog_independent %>% 
  group_by(GroupAssignment) %>% 
  summarise(n = n(), 
            mean_Flourishing = mean(Flourishing_post),
            sd_Flourishing = sd(Flourishing_post)) %>% 
  ungroup()

Task 6: Check assumptions

Assumption 1: Continuous DV

Is the dependent variable (DV) continuous? Answer:

Assumption 2: Data are independent

Each observation in the dataset has to be independent, meaning the value of one observation does not affect the value of any other. Answer:

Assumption 3: Homoscedasticity (homogeneity of variance)

I’ve computed Levene’s test below. How do you interpret the output?

leveneTest(Flourishing_post ~ GroupAssignment, data = dog_independent)
Df F value Pr(>F)
group 1 0.7111707 0.4001329
187 NA NA
Answer:

Assumption 4: DV should be approximately normally distributed

Looking at the violin-boxplot below, are both groups normally distributed?

ggplot(dog_independent, aes(x = GroupAssignment, y = Flourishing_post, fill = GroupAssignment)) +
  geom_violin(alpha = 0.4) +
  geom_boxplot(width = 0.3, alpha = 0.8) +
  scale_fill_viridis_d(option = "cividis", guide = "none") +
  theme_classic() +
  labs(x = "Group", y = "Psychological well-being (post-intervention)")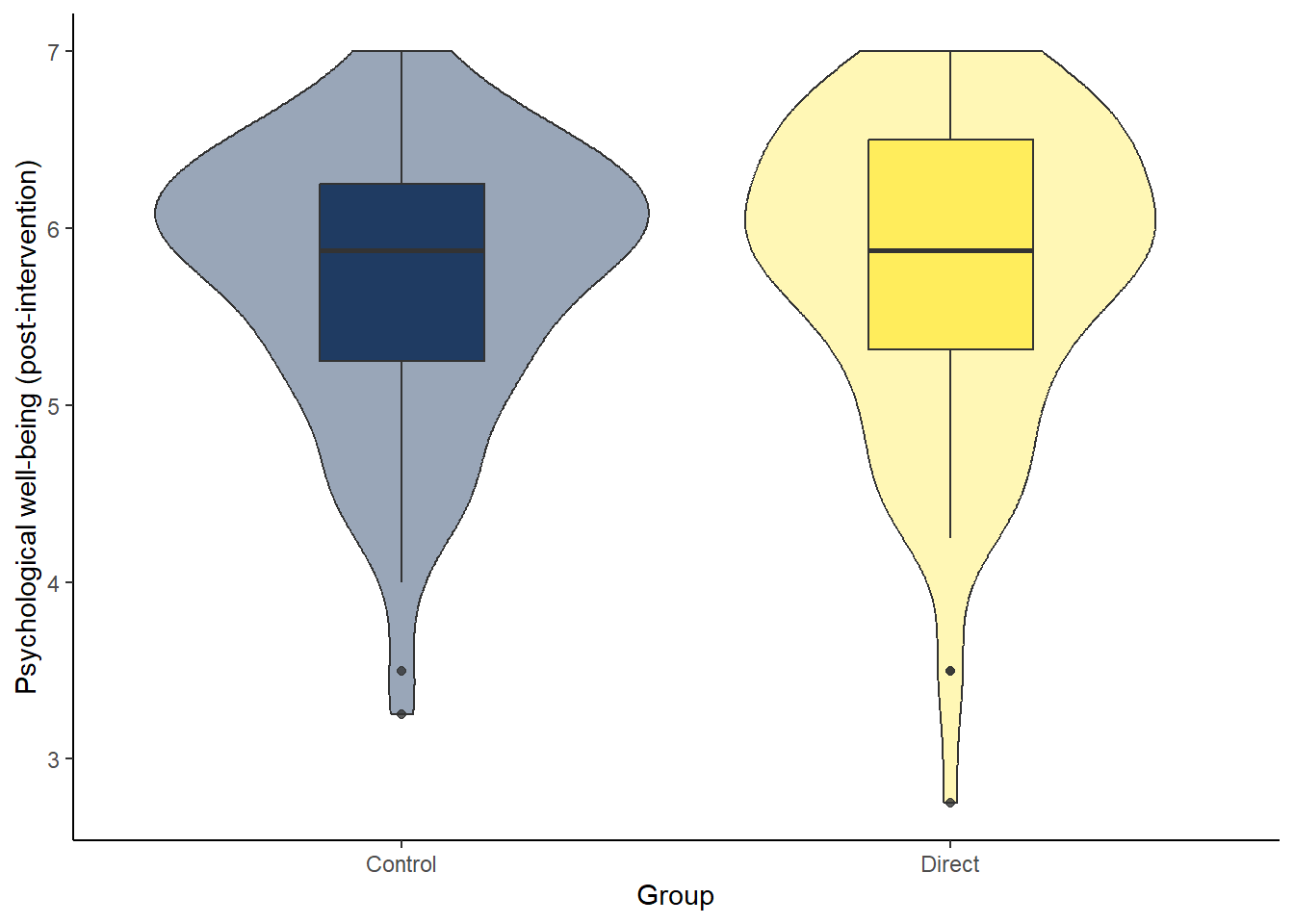

Answer:

Conclusion from assumption tests

With all assumptions tested, which statistical test would you recommend for this analysis?

Answer:

Task 7: Computing a two-sample t-test with effect size & interpret the output

  • Step 1: Compute the Welch two-sample t-test. The structure of the function is as follows:
t.test(DV ~ IV, data = your_dataframe, var.equal = FALSE, alternative = "two.sided")
t.test(Flourishing_post ~ GroupAssignment, data = dog_independent, var.equal = FALSE, alternative = "two.sided")
  • Step 2: Calculate an effect size

Calculate Cohen’s D. The structure of the function is as follows:

cohensD(DV ~ IV, data = your_dataframe, method = "unequal")
cohensD(Flourishing_post ~ GroupAssignment, data = dog_independent, method = "unequal")
  • Step 3: Interpreting the output

Below are the outputs for the descriptive statistics (table), Welch t-test (main output), and Cohen’s D (last line starting with [1]). Based on these, write up the results in APA style and provide an interpretation.

GroupAssignment n mean_Flourishing sd_Flourishing
Control 94 5.718085 0.7709738
Direct 95 5.776316 0.8638912 

    Welch Two Sample t-test

data:  Flourishing_post by GroupAssignment
t = -0.48902, df = 185.05, p-value = 0.6254
alternative hypothesis: true difference in means between group Control and group Direct is not equal to 0
95 percent confidence interval:
 -0.2931533  0.1766920
sample estimates:
mean in group Control  mean in group Direct 
             5.718085              5.776316 

[1] 0.0711213

The Welch two-sample t-test revealed that there is in psychological well-being scores between direct (N = , M = , SD = ) and control group (N = , M = , SD = ), t() = , p = , V = . The strength of the association between the variables is considered . We therefore .

Test your knowledge

Question 1

What is the main purpose of an independent t-test?

The independent t-test is specifically designed to compare the means of two separate (independent) groups to determine whether the difference between their means is statistically significant. For example, it could be used to compare the test scores of students who received two different teaching methods (Group 1 vs. Group 2).

Question 2

Which of the following is a key assumption of the two-sample t-test that should be considered?

Independence of observations is a crucial assumption for the two-sample t-test. It means that the data collected from one participant should not influence the data from another participant.

Question 3

How can you recognise the difference between the output of a Student’s t-test and a Welch t-test?

The Welch t-test adjusts for unequal variances and sample sizes, which leads to non-integer degrees of freedom. In contrast, the Student’s t-test assumes equal variances and reports integer degrees of freedom based on total sample size minus the number of groups.

The other options are incorrect:

  • Both tests report confidence intervals for the mean difference.
  • Both tests compare means, not medians.
  • Neither test reports effect size directly; it must be calculated separately (e.g., using Cohen’s d).

Question 4

You perform an independent t-test and find \(t(48)=2.10,p=.042,d=0.58\). How would you interpret these results?

The p-value (\(p=.042\)) is less than the common significance threshold of 0.05, indicating that the difference between the two groups is statistically significant. This means we reject the null hypothesis and conclude that there is evidence of a difference between the group means.