9  Correlations

Intended Learning Outcomes

By the end of this chapter you should be able to:

  • Compute a Pearson correlation and effectively report the results.
  • Understand when to use a non-parametric equivalent of correlation, compute it, and report the results.

Individual Walkthrough

9.1 Activity 1: Setup & download the data

This week, we will be working with a new dataset. Follow the steps below to set up your project:

  • Create a new project and name it something meaningful (e.g., “2A_chapter9”, or “09_correlation”). See Section 1.2 if you need some guidance.
  • Create a new .Rmd file and save it to your project folder. See Section 1.3 if you need help.
  • Delete everything after the setup code chunk (e.g., line 12 and below)
  • Download the new dataset here: data_ch9.zip. The zip folder includes the following files:
    • Soupbowl_data_dictionary.xlsx: A codebook with detailed variable descriptions
    • data_ch9_correlation.csv: A CSV file containing data from the experiment and demographic information
    • A copy of the paper by Lopez et al. (2024) and the Supplementary materials
  • Extract the data files from the zip folder and place them in your project folder. If you need help, see Section 1.4.

Citation

Lopez, A., Choi, A. K., Dellawar, N. C., Cullen, B. C., Avila Contreras, S., Rosenfeld, D. L., & Tomiyama, A. J. (2024). Visual cues and food intake: A preregistered replication of Wansink et al. (2005). Journal of Experimental Psychology: General, 153(2), 275–281. https://doi.org/10.1037/xge0001503

The preregistration, data and supplementary materials are available on OSF & APA’s “Journal of Experimental Psychology: General”:

Abstract

Imagine a bowl of soup that never emptied, no matter how many spoonfuls you ate—when and how would you know to stop eating? Satiation can play a role in regulating eating behavior, but research suggests visual cues may be just as important. In a seminal study by Wansink et al. (2005), researchers used self-refilling bowls to assess how visual cues of portion size would influence intake. The study found that participants who unknowingly ate from self-refilling bowls ate more soup than did participants eating from normal (not self-refilling) bowls. Despite consuming 73% more soup, however, participants in the self-refilling condition did not believe they had consumed more soup, nor did they perceive themselves as more satiated than did participants eating from normal bowls. Given recent concerns regarding the validity of research from the Wansink lab, we conducted a preregistered direct replication study of Wansink et al. (2005) with a more highly powered sample (N =464 vs. 54 in the original study). We found that most results replicated, albeit with half the effect size (d= 0.45 instead of 0.84), with participants in the self-refilling bowl condition eating significantly more soup than those in the control condition. Like the original study, participants in the selfrefilling condition did not believe they had consumed any more soup than participants in the control condition. These results suggest that eating can be strongly controlled by visual cues, which can even override satiation.

Public Significance Statement

Results from this study are relevant to public health and science given the influence that the bottomless soup bowls study had on public policy and the skepticism surrounding research from the Wansink lab. We found that what the eyes see plays a significant role in how much people eat and how full they feel. Given the high prevalence of diseases of overconsumption, this study has implications for the regulation of eating behavior.

Changes made to the dataset

  • The basis for data_ch9_correlation.csv is the file named included&excludedFINAL.sav on OSF. It contains 632 observations.
  • The original authors used an SPSS file format, which was exported as a csv.
  • The original authors coded missing values as 999 and 888. These were replaced with actual missing values (NA).
  • Variables M_postsoup and Condition were removed so we can practice more data wrangling. It also gives us an opportunity to include one of Gaby’s favourite functions coalesce().
  • No other changes were made.

9.2 Activity 2: Library and data for today

Today, we will use the following packages: tidyverse, ggExtra, correlation, qqplotr, and pwr. As always, you may need to install any packages you have not used/ installed before (see Section 1.5.1 if you need some help).

Additionally, we will read in today’s data from data_ch9_correlation.

# load in the packages
???

# read in the data
lopez_data <- ???
# load in the packages
library(tidyverse)
library(ggExtra)
library(correlation)
library(qqplotr)
library(pwr)

# read in the data
lopez_data <- read_csv("data_ch9_correlation.csv")

9.3 Activity 3: Familiarise yourself with the data

As usual, take some time to familiarise yourself with the data before starting the analysis. Review the codebook to understand the variables and their measurement.

We notice that lopez_data contains data from 632 participants, whereas the Lopez et al. (2024) paper reports a total of 654 participants. Have a look at the data and the paper. Can you explain the discrepancy?

Lopez et al. appear to have published data for both the participants included in the final sample (464 participants) and those excluded after discovering the true purpose of the study (168 participants). However, an additional 22 participants were excluded due to experimenter error, and their data were not recorded.

Today, we will focus on a few correlation values and attempt to reproduce some of the results presented in Table 2 of Lopez et al. (2024).

Table 2 (Lopez et al., 2024)

As shown in the table above, the original authors aimed to replicate the correlations reported by Wansink et al. (2005). Specifically, they examined the following relationships:

  • Estimated ounces of soup consumed with actual consumption volume
  • Estimated calories of soup consumed with actual consumption volume

These correlations were calculated for three groups: participants who ate from normal bowls, participants who ate from self-refilling bowls, and the combined group of all participants.

9.4 Activity 4: Preparing the dataframe

To calculate correlations, the data must be in wide format. Fortunately, lopez_data is already in wide format. However, if your data is organised differently, ensure that each variable is in its own column.

Step 1: Excluding participants’ data

Check that only participants who meet the recruitment criteria are included, and exclude those who do not. Lopez and colleagues made this straightforward by including the variable Included in the dataset. This variable indicates which participants were included in the final dataset (value of 1) and which were excluded (value of 0). After completing this step, our new data object should contain 464 participants.

Create a new data object named lopez_included that contains only the participants marked as included in the final dataset (i.e., those with a value of 1 in the Included variable).

lopez_included <- lopez_data %>% 
  filter(Included == 1)

Step 2: Selecting relevant variables

Big datasets can be messy, so it is often helpful to focus only on the variables relevant to your analysis. For this task, we want to include the following variables:

  • ParticipantID
  • Estimated ounces of food consumed (OzEstimate)
  • Estimated calories of food consumed (CalEstimate)
  • Consumption volume - Experimental soup intake (ExpSoupAte)
  • Consumption volume - Control soup intake (CtrlSoupAte)
  • SeatPosition - so we can determine whether participants were sorted into in the Experimental or the Control group

Store the new data object as lopez_reduced.

lopez_reduced <- lopez_included %>% 
  select(ParticipantID, Sex, OzEstimate, CalEstimate, CtrlSoupAte, ExpSoupAte, SeatPosition)

Step 3: Recoding the values

As we can see now, our lopez_reduced data object could use some tidying.

  1. Sex is a categorical variable, yet, it is currently displayed as numeric, which isn’t ideal. Recode these values according to the Soupbowl_data_dictionary. You could either recode the values as we did in Section 3.3) or convert Sex into a factor if that’s easier (see Chapter 4 for guidance).
  2. ParticipantID should also be converted into a factor (see Chapter 4 for guidance).
  3. Create a new variable called Condition to indicate whether participants are in the Control or Experimental group. Use the Soupbowl_data_dictionary o determine which SeatPosition corresponds to normal bowls (Control) and self-refilling bowls (Experimental). If you’re unsure which function to use, refer to Section 3.4.
  4. CtrlSoupAte and ExpSoupAte can remain separate if we want to focus on these two conditions individually, as we can remove missing values later. However, to calculate correlations across the whole sample, we need these “SoupAte” values in a single column instead of two. We will name this coalesced variable M_postsoup to align with the Soupbowl_data_dictionary.

You should be able to complete recoding tasks 1, 2, and 3 on your own. However, Task 4 involves a new function, so we will walk through it together.

In the panels below, I have created new variables in lopez_reduced to show you solutions for both the case_match() and the factor() approach for recoding Sex. Alternatively, you could simply name your new column Sex to overwrite the numeric values in the existing Sex column.

Since no conditional statement is needed, a simple case_match() will suffice. This will create a character column.

lopez_reduced <- lopez_reduced %>% 
  mutate(Sex_case_match = case_match(Sex,
                                     0 ~ "Male",
                                     1 ~ "Female",
                                     2 ~ "Other",
                                     3 ~ "Prefer not to say"))

Using a factor is helpful if you want to reorder the labels simultaneously. This will create a factor column.

lopez_reduced <- lopez_reduced %>% 
  mutate(Sex_factor = factor(Sex,
                         levels = c(1, 0, 2, 3),
                         labels = c("Female", "Male", "Other", "Prefer not to say")))

There is not much to it, as the levels and labels don’t need changing.

lopez_reduced <- lopez_reduced %>% 
  mutate(ParticipantID = factor(ParticipantID))

According to the Soupbowl_data_dictionary, even numbers in SeatPosition indicate the Experimental group, and odd numbers represent the Control group. Here we will need to use case_when() because conditional statements (see Chapter 3 Activity 4 for a refresher).

lopez_reduced <- lopez_reduced %>% 
  mutate(Condition = case_when(
    SeatPosition %in% c(1,3) ~ "Control",
    SeatPosition %in% c(2,4) ~ "Experimental"
  ))
Note

In the code, I specified 1 and 3 should be labelled “Control” and 2 and 4 “Experimental”. I could have used with the .default = argument for the even seat numbers, however, this requires being certain that all other values are either 2 or 4 (e.g., no invalid numbers like 5 or missing values). Since I did not check beforehand, any value that is not 1, 2, 3, or 4 will remain unlabelled, making it easier to identify and address.

We want to combine the values from CtrlSoupAte and ExpSoupAte into a single column named M_postsoup. (No idea why the authors called it M_postsoup rather than AllSoupAte. However, since this was one of the columns deleted from the original dataset earlier, we’ll stick with the original variable name as the authors intended.)

Recoding task 4 is straightforward with a function like coalesce(). For each row, it checks the specified columns and finds the first non-missing value at each position. Essentially, R scans the columns row by row, looking for the first available value that isn’t missing and assigns it to the new column. For example:

  • Participant 1001 has no value in CtrlSoupAte but has a value in ExpSoupAte, so R skips the missing value and assigns 4.5 to the new column.
  • Participant 1002 has a value in CtrlSoupAte (3.3), directly assigns it to the new column, and so on.
lopez_reduced <- lopez_reduced %>% 
  mutate(M_postsoup = coalesce(CtrlSoupAte, ExpSoupAte))

As always, all these “preparing the dataframe” steps could have been combined into a single pipe.

lopez_reduced <- lopez_data %>% 
  # Step 1
  filter(Included == 1) %>% 
  #Step 2
  select(ParticipantID, Age, Sex, OzEstimate, CalEstimate, CtrlSoupAte, ExpSoupAte, SeatPosition) %>% 
  # Step 3 (I decided to use the factor approach and override my `Sex` column and include it all into the same `mutate()` function)
  mutate(Sex = factor(Sex,
                      levels = c(1, 0, 2, 3),
                      labels = c("Female", "Male", "Other", "Prefer not to say")),
         ParticipantID = factor(ParticipantID),
         Condition = case_when(
           SeatPosition %in% c(1,3) ~ "Control",
           SeatPosition %in% c(2,4) ~ "Experimental"),
         # Step 4
         M_postsoup = coalesce(CtrlSoupAte, ExpSoupAte))

9.5 Activity 5: Compute descriptives

Now that the data is ready, we can focus on reproducing the correlations. For the remainder of this chapter, we will focus on correlating the estimated ounces of soup consumption with actual consumption volume for the control group. Testing every correlation would require assessing assumptions for each relationship, making this chapter unnecessarily long. However, you are welcome to reproduce all other correlations in your own time if you wish.

For the descriptives, we will compute the number of participants (n), means and standard deviations for the Control group of our variables of interest (i.e., CalEstimate and M_postsoup).

  • Filter the data to include only the Control group and focus on the two variables of interest (CalEstimate and M_postsoup), and keep the ParticipantID. You may want to store the data as a new object named lopez_control.
  • Watch out for missing values in some of the columns. We will address them later during the correlation analysis. For now, instruct R to ignore missing values when calculating descriptive statistics.
## data object lopez_control
lopez_control <- lopez_reduced %>% 
  filter(Condition == "Control") %>% 
  select(ParticipantID, CalEstimate, M_postsoup)

# descriptives for lopez_control
descriptives_control <- lopez_control %>% 
  summarise(n = n(),
            mean_CalEstimate = mean(CalEstimate, na.rm = TRUE),
            sd_CalEstimate = sd(CalEstimate, na.rm = TRUE),
            mean_M_postsoup = mean(M_postsoup),
            sd_M_postsoup = sd(M_postsoup)) %>% 
  ungroup()

descriptives_control
n mean_CalEstimate sd_CalEstimate mean_M_postsoup sd_M_postsoup
246 133.0328 121.3261 8.86748 6.236679

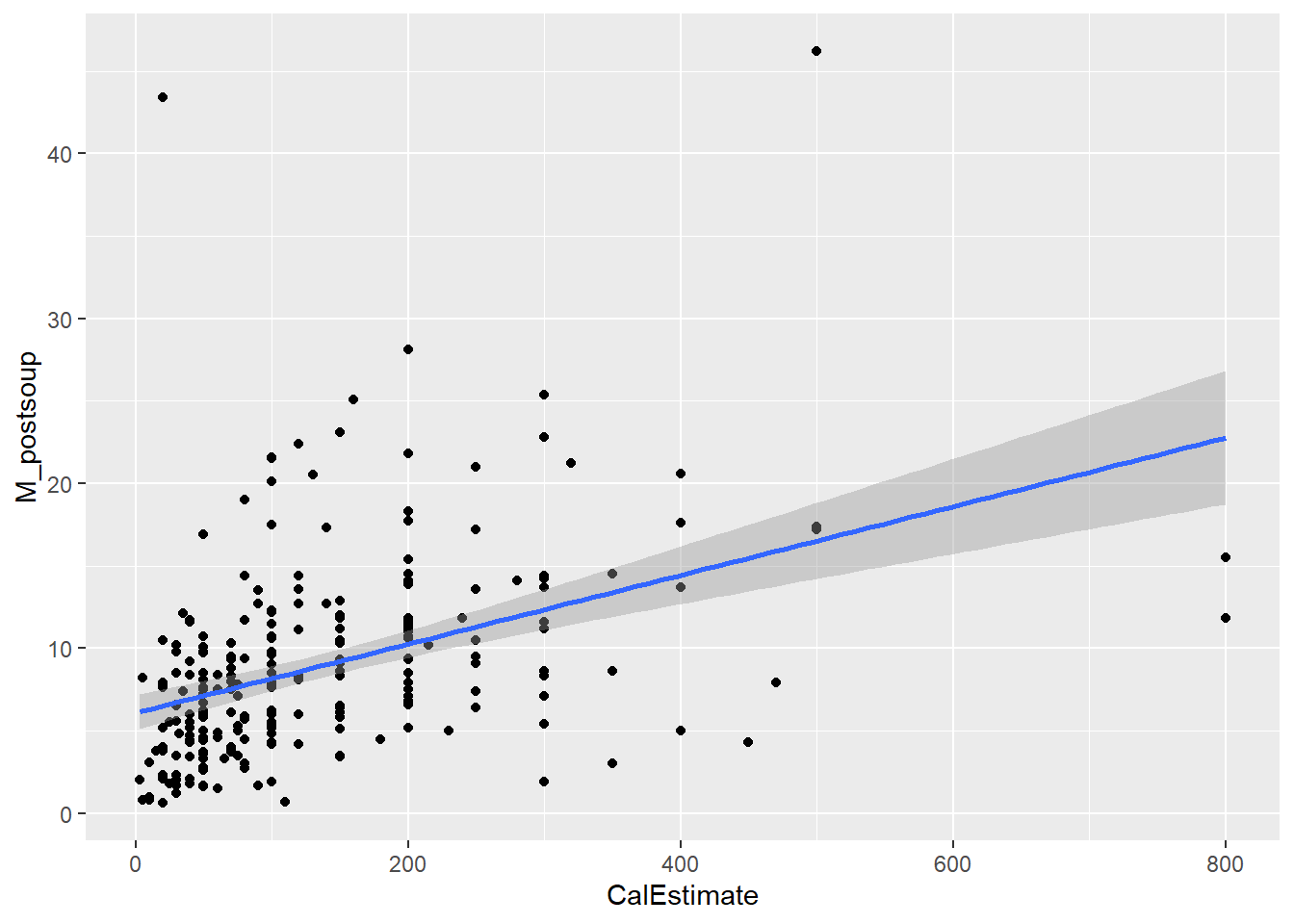
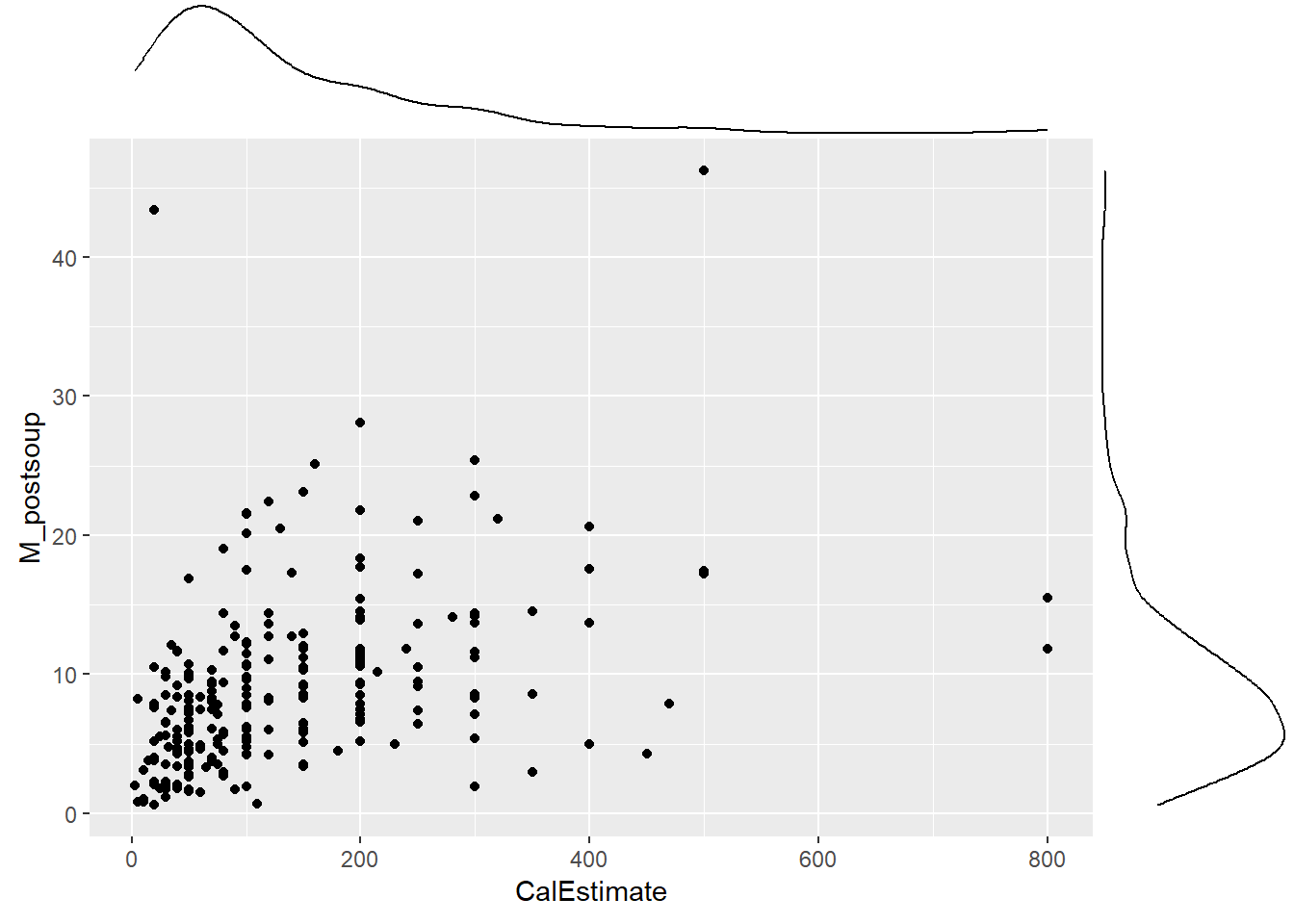
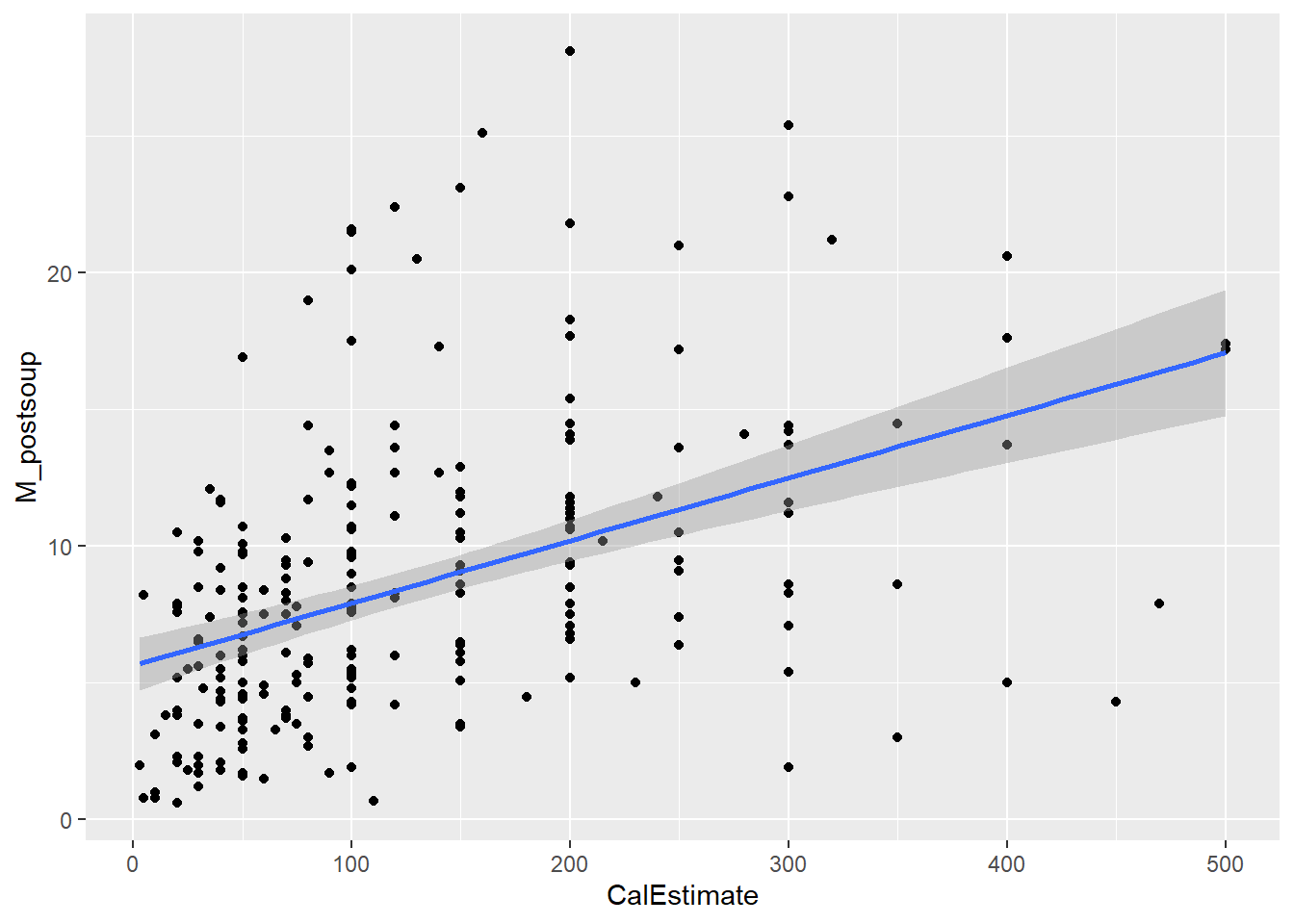
9.6 Activity 6: Create an appropriate plot

The only option for a correlation is a because .

Create an appropriate plot to visualise the relationship between CalEstimate and M_postsoup.

ggplot(lopez_control, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "lm")
`geom_smooth()` using formula = 'y ~ x'
Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_smooth()`).
Warning: Removed 2 rows containing missing values or values outside the scale range
(`geom_point()`).

9.7 Activity 7: Check assumptions

Assumption 1: Continuous variables

Both variables must be measured at the interval or ratio level (i.e., continuous data). We can confirm this by examining our two variables of interest, CalEstimate and M_postsoup. Plus, you would already know whether the variables are continuous based on your study design.

Assumption 3: Independence of cases/observations

Similar to the paired t-test, we must assume that the two observations for each case are independent of the observations for any other case. This basically means that participants did not influence each other’s ratings. Once again, this assumption is related to the study design and is satisfied in this instance.

Assumption 4: Linearity

To run a Pearson correlation, the relationship between the two variables must be linear.

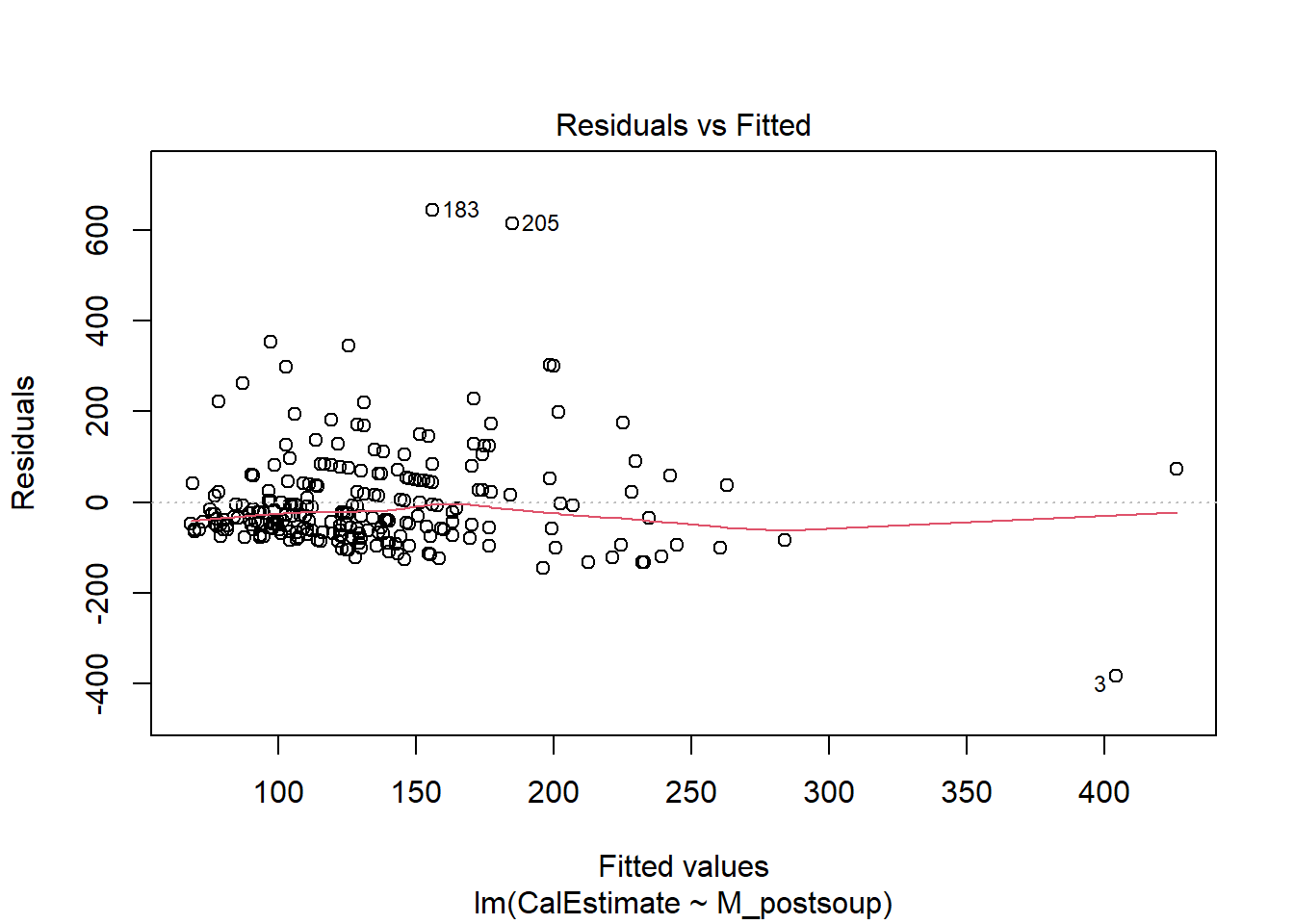
You can assess linearity visually using a Residuals vs Fitted plot, which can be generated by applying the plot() function to a linear model (lm) object. The function requires the following arguments:

  • The 2 variables of interest, separated by a tilde (~)
  • The dataset
  • The which argument specifies which plot we want to show. Number 1 will produce a Residuals vs Fitted plot.
plot(lm(CalEstimate~M_postsoup, data = lopez_control_no_na), which = 1)

You can also assess linearity using a scatterplot, but instead of fitting a linear model “lm”, use the “loess” method for the line of best fit. Then, examine how closely the resulting line resembles a linear line.

ggplot(lopez_control_no_na, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "loess")
`geom_smooth()` using formula = 'y ~ x'

Verdict: This does actually look non-linear to me. The original authors did not mention any assumption testing in their paper or Supplementary Materials. If they conducted these tests, we can assume they deemed the assumptions satisfied.

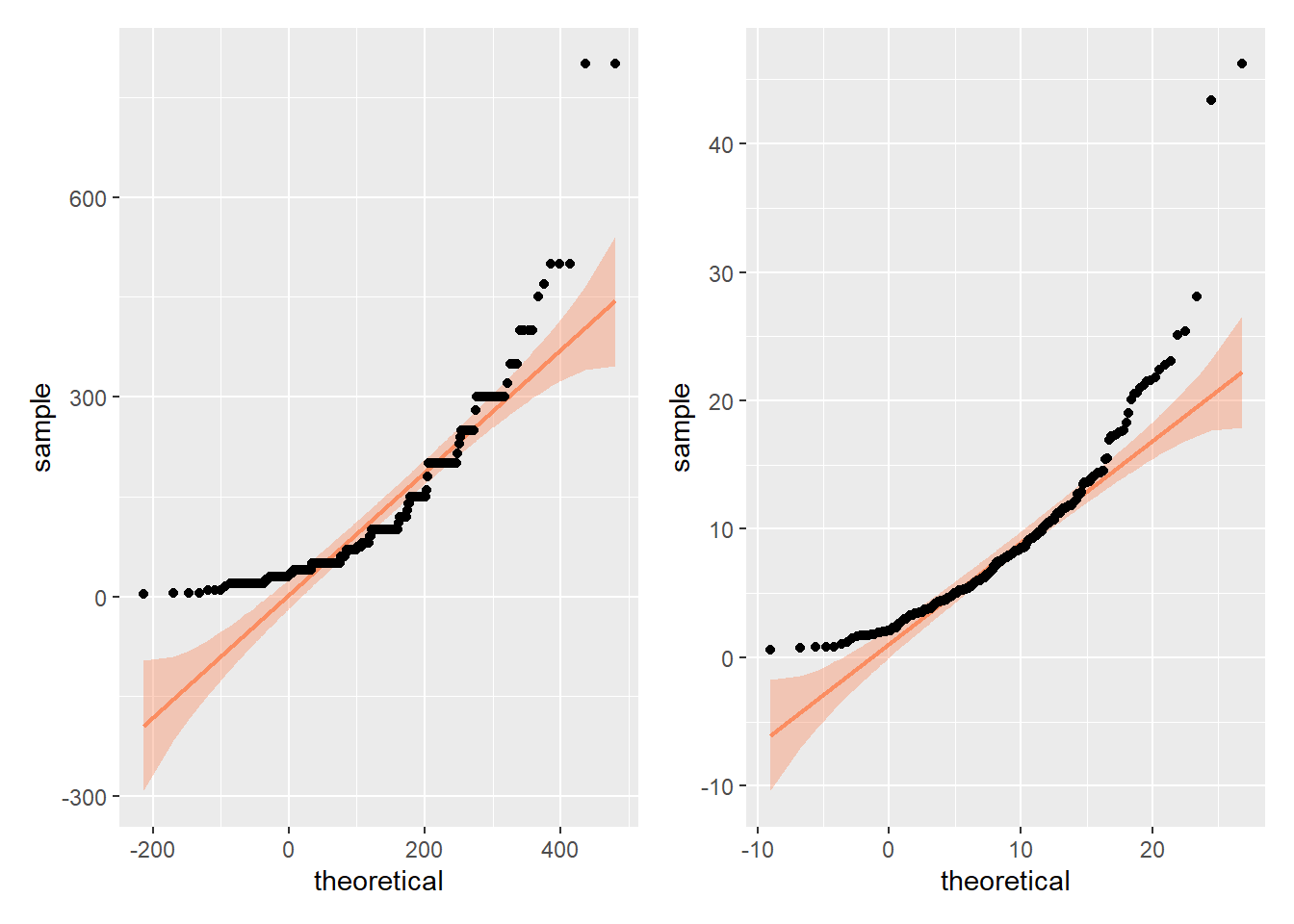
Assumption 5: Normality

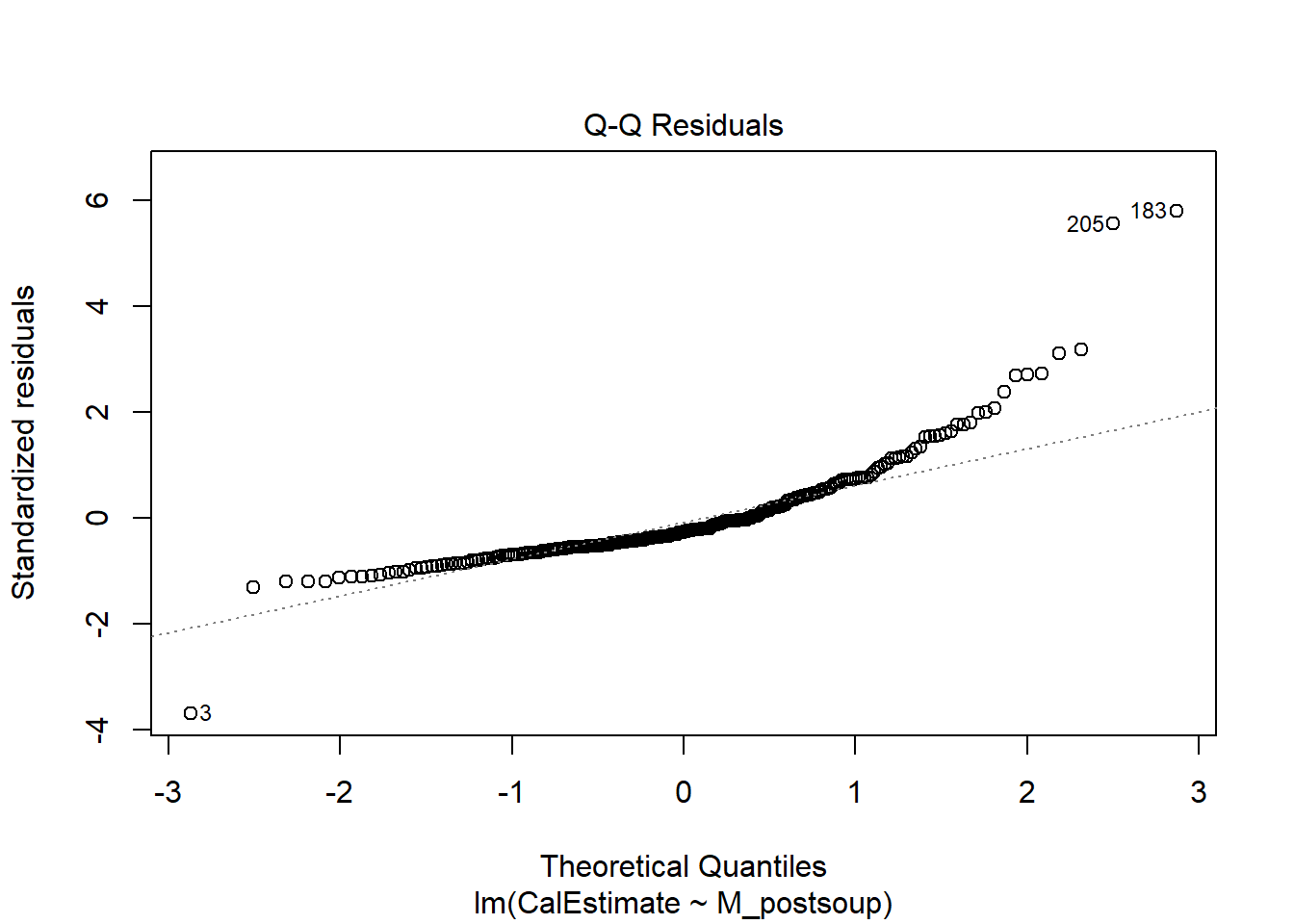
Residuals for both variables should follow a bivariate normal distribution (i.e., both together normally distributed). We can use a Q-Q plot to visually check this assumptions. The code is the same as above (i.e., plot() with lm()), but this time, set the which argument to 2 to generate the Q-Q plot.

plot(lm(CalEstimate~M_postsoup, data = lopez_control_no_na), which = 2)

In practice it is frequently accepted that each variable is normally distributed rather than both together (i.e., univariate normality). However, there is some disagreement among experts whether Pearson’s correlation is “robust” to violations of univariate normality. Anyway, we are showing this approach as an alternative using the Q-Q plot version with packages ggplot and qqplotr.

ggplot(lopez_control_no_na, aes(sample = CalEstimate)) +
  stat_qq_band(fill = "#FB8D61", alpha = 0.4) +
  stat_qq_line(colour = "#FB8D61") +
  stat_qq_point()

ggplot(lopez_control_no_na, aes(sample = M_postsoup)) +
  stat_qq_band(fill = "#FB8D61", alpha = 0.4) +
  stat_qq_line(colour = "#FB8D61") +
  stat_qq_point()

Figure 9.1: Bins vs binwidth arguments

We can also use the function ggMarginal() to enhance a ggplot2 scatterplot by adding marginal density plots, histograms, or boxplots. The workflow is slightly different: first, save the scatterplot as a data object, then apply ggMarginal() to that object.

To customise the marginal plots:

  • Use type = "histogram" for histograms.
  • Use type = "boxplot" for boxplots.
  • Leave the type argument out or set it to type = "density" to display the default density plots.
p1 <- ggplot(lopez_control_no_na, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point()

ggMarginal(p1, type = "density")

More info here: https://cran.r-project.org/web/packages/ggExtra/vignettes/ggExtra.html

Verdict: For me, the assumption of normality would not hold, whether assessed jointly or independently, as the points follow a curve rather than “hugging” the straight line with potentially some potential deviations in the tails. However, I seem to be more conservative in my judgements compared to Lopez et al. Since they proceeded with a Pearson correlation, the assumption must have held for them.

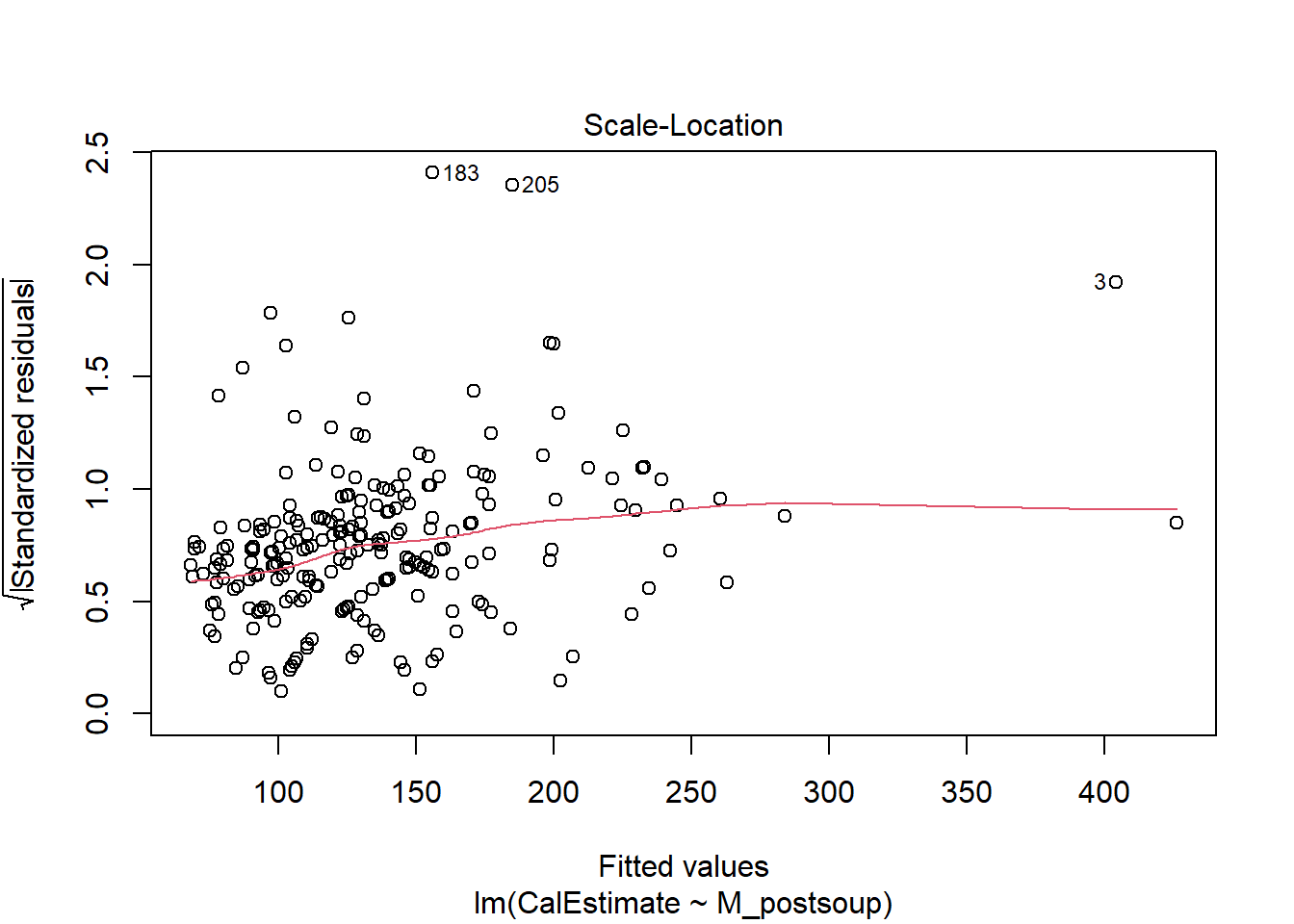
Assumption 6: Homoscedasticity

Homoscedasticity assumes that the data is evenly distributed around the line of best fit, with no visible pattern. This assumption can be assessed visually using a Scale-Location plot or directly within the scatterplot.

As you might have guessed, we will use the plot() function with lm() again but this time set the which argument to 3 to generate the Scale-Location plot.

plot(lm(CalEstimate~M_postsoup, data = lopez_control_no_na), which = 3)

We will use the same scatterplot as above, but this time focus on the points and their distance from the blue line. If the points are randomly scattered around the line of best fit, the assumption holds. However, if a distinct pattern emerges, the assumption is violated.

ggplot(lopez_control_no_na, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "lm")
`geom_smooth()` using formula = 'y ~ x'

Verdict: This is another assumption that feels borderline to me. There appears to be slight heteroscedasticity. In the Scale-Location plot, the red line should ideally be flat and horizontal, but ours has a slight slope and could be flatter. If you prefer looking at the scatterplot, you can observe the data points moving slightly further away from the line of best fit as the x and y values increase. this is kinda forming a slight funnel shape rather than the roughly random spread of data points shown in last week’s lecture slides. Nevertheless, the authors took a more lenient approach and considered the assumption to be met.

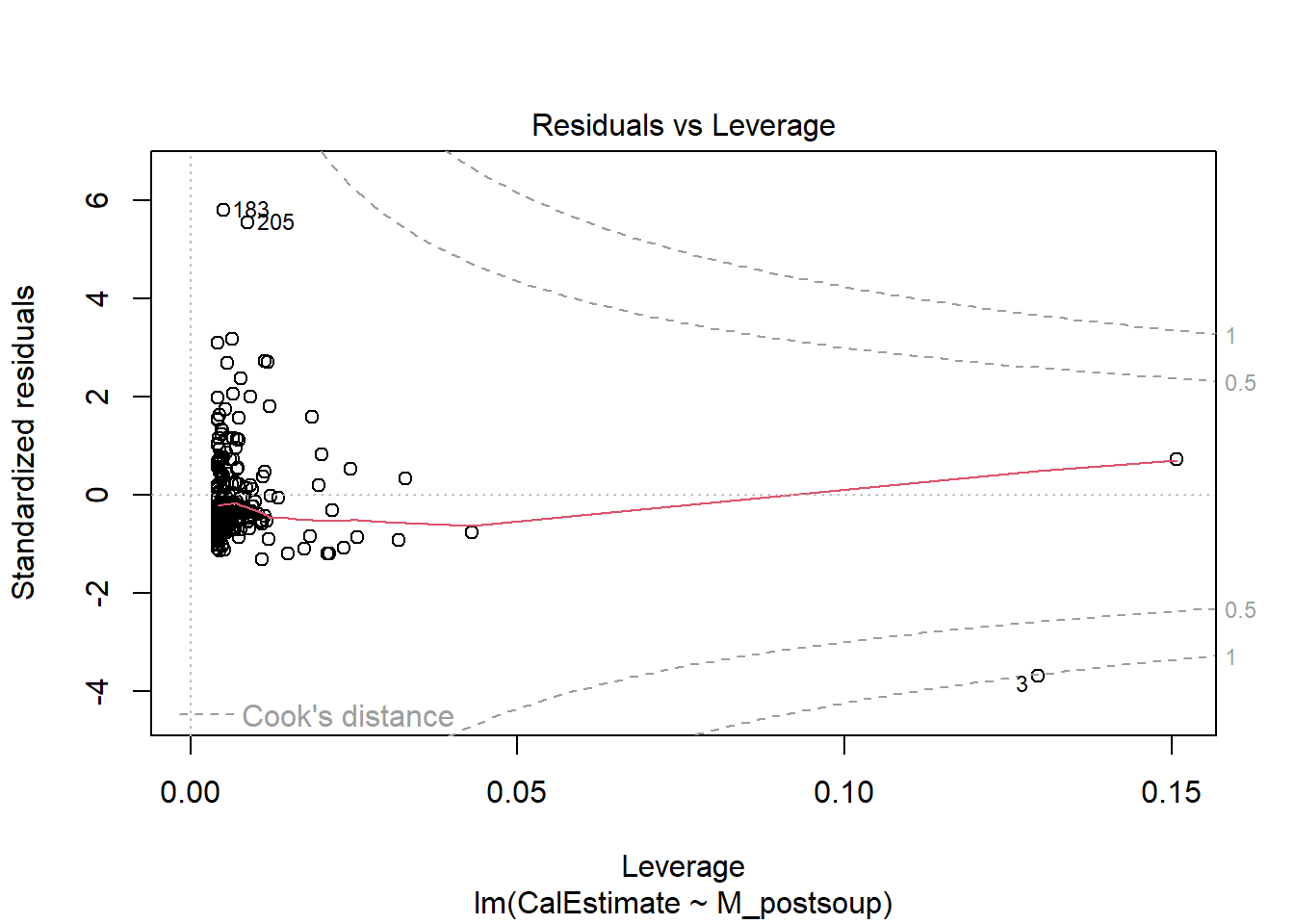
Assumption 7: Absence of outliers

Ideally, our data should not contain any outliers or influential points, as these can distort the relationship between the variables of interest. We can assess this assumption visually with a Residuals vs Leverage plot or by revisiting the scatterplot (as shown above).

To identify those data points, we can look at plot 5 from the plot() function with the lm() object but setting the which argument to 5.

plot(lm(CalEstimate~M_postsoup, data = lopez_control_no_na), which = 5)

Here, case numbers 3, 183, and 205 are identified. In the data object lopez_control_no_na, these correspond to participant IDs 1007, 1716, and 1789, respectively. Two of these participants estimated they had consumed 800 calories, while the third data point has a y-value over 40 (the one with the lower x-value).

Looking at the scatterplot, I would have probably identified 4 outliers - anyone who estimated more than 600 cal and anyone who consumed more than 40 ounces of soup.

Verdict: There are several ways to handle outliers, such as excluding them, replacing their extreme values with the group mean, or winsorising them. For now, I would likely exclude these three data points from the dataset before proceeding. However, Lopez et al. chose to retain all data points.

Remember: Any data exclusions in your reports must be clearly justified.

Your Turn

Filter out the 3 (or 4) influential points/outliers and create the plot again. It’s best to save the data without outliers as a new data object. I’ve named mine lopez_control_no_outliers, but feel free to use a name that works for you.

lopez_control_no_outliers <- lopez_control_no_na %>% 
  filter(!ParticipantID %in% c(1007, 1716, 1789))
ggplot(lopez_control_no_outliers, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "lm")
`geom_smooth()` using formula = 'y ~ x'

lopez_control_no_outliers4 <- lopez_control_no_na %>% 
  filter(CalEstimate < 600,
         M_postsoup < 40)
ggplot(lopez_control_no_outliers4, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "lm")
`geom_smooth()` using formula = 'y ~ x'

Final word on Assumption checks

For me, there would be enough justification to switch to a non-parametric correlation method, such as Spearman. However, since the original authors ran Pearson correlations, we will follow their approach in Activity 8. We will also revert to the data object lopez_control, as the original authors chose not to exclude any data points (e.g., missing values, outliers, etc.).

9.8 Activity 8: Pearson’s correlation & effect size

There are plenty of options out there to compute a correlation. We will use the correlation() function from the correlation package because it offers more consistent reporting features. The correlation() function requires:

  • The name of the data set you are using.
  • The name of the first variable you want to select for the correlation.
  • The name of the second variable you want to select for the correlation.
  • The type of correlation you want to run: e.g. Pearson, Spearman.

For a two-tailed Pearson correlation using the lopez_control dataset, the code would look like this (note the quotation marks around everything except the data object):

correlation(data = lopez_control,
            select = "CalEstimate",
            select2 = "M_postsoup",
            method = "Pearson",
            alternative = "two.sided")
Parameter1 Parameter2 r CI CI_low CI_high t df_error p Method n_Obs
CalEstimate M_postsoup 0.4045319 0.95 0.293876 0.5044879 6.881219 242 0 Pearson correlation 244
Tip

Since lopez_control contains only three variables and we’ve already converted ParticipantID into a factor, we can pass the entire data object to the correlation() function. This will compute correlations between all numeric columns in the dataset. In this case, it would result in just one association, but see below for an example with more numeric variables.

correlation(lopez_control)
Parameter1 Parameter2 r CI CI_low CI_high t df_error p Method n_Obs
CalEstimate M_postsoup 0.4045319 0.95 0.293876 0.5044879 6.881219 242 0 Pearson correlation 244

Here we obtained a Pearson correlation value of .405 which is close to the value of .41 reported by Lopez et al. (2024). Remember to report correlation values to three decimal places to adhere to APA style (though the journal in this case may have followed different guidelines).

If you want to correlate multiple variables with one another, you can do that in a correlation matrix.

Let’s try to replicate the correlations for full sample:

  • OzEstimate and CalEstimate,
  • OzEstimate and M_postsoup, and
  • CalEstimate and M_postsoup.

To do this, first ensure that only the relevant variables are selected and that a variable like ParticipantID is converted into a factor. I have stored all four variables in an object called lopez_overall.

You can also include an additional argument, p_adjust, to specify the type of correction you want to apply for multiple comparisons (e.g., “Bonferroni”). If you don’t include the p_adjust argument, the default method will be “Holm”. In either case, the correction method will be listed in the output.

lopez_overall <- lopez_reduced %>% 
  select(ParticipantID, OzEstimate, CalEstimate, M_postsoup)

correlation(lopez_overall, p_adjust = "bonferroni")
Parameter1 Parameter2 r CI CI_low CI_high t df_error p Method n_Obs
OzEstimate CalEstimate 0.2575243 0.95 0.1700045 0.3410133 5.697404 457 1e-07 Pearson correlation 459
OzEstimate M_postsoup 0.2829064 0.95 0.1967556 0.3647221 6.326103 460 0e+00 Pearson correlation 462
CalEstimate M_postsoup 0.3611089 0.95 0.2789816 0.4379921 8.296305 459 0e+00 Pearson correlation 461
Important

When running the code in the .Rmd file, the correction method is displayed beneath the table in the printout. However, when the document is knitted into HTML, this information does not appear.

However, in the knitted document, the output also includes the number of observations for each row, whereas the .Rmd printout only displays the range of observation values beneath the table.

Similarly, p-values are displayed in APA style (e.g., p < .001) in the .Rmd printout, but in the knitted document, they may appear in scientific notation or as 0. When reporting p-values in your report, ensure they adhere to APA style.

The effect size for correlations does not require additional computation. It is simply the vale of the correlation coefficient r.

9.9 Activity 9: Sensitivity power analysis

As with the t-test, we will conduct a sensitivity power analysis to determine the minimum effect size detectable with our sample of control participants (n = 244, accounting for the two missing values), an alpha level of 0.05, and a power of 0.8. This will help us assess whether our analysis was sufficiently powered.

We will use the pwr.r.test() function from the pwr package for the correlation analysis. As usual, include n, alpha, and power as arguments in the function, and leave out the effect size r.

pwr.r.test(n = 244, sig.level = 0.05, power = 0.8, alternative = "two.sided")

     approximate correlation power calculation (arctangh transformation) 

              n = 244
              r = 0.1782315
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

According to the output above, the smallest r detectable with 244 participants, a significance level of .05, and a power of .8 is .178. Since Lopez et al. reported an effect size of r = .41, the study was sufficiently powered.

9.10 Activity 10: The write-up

Lopez et al. (2024) hypothesised a positive correlation between estimated calories of soup consumed \((M = 133.0 cal, SD = 121.3 cal)\) and actual consumption volume \((M = 8.87 oz, SD = 6.24 oz)\). A Pearson correlation revealed a moderately strong, positive, and statistically significant relationship between these two variables, \(r(242) = .405, p < .001, 95\% CI = [.294, .504]\). The study was sufficiently powered. Lopez et al. rejected the null hypothesis in favour of H1.

9.11 Activity 11: Non-parametric alternative

Running a Pearson correlation when its assumptions are violated can lead to unreliable and misleading results, meaning the calculated correlation coefficient may not accurately reflect the true relationship between the variables.

The non-parametric alternative is Spearman’s Rank correlation. However, Spearman’s correlation also has a few assumptions:

  • Both variables must be measured on ordinal, interval or ratio scales.
  • There must be a monotonic relationship between the two variables, meaning they are either positively or negatively correlated. The data points should not display a “U-shape” or an “inverted U-shape”.

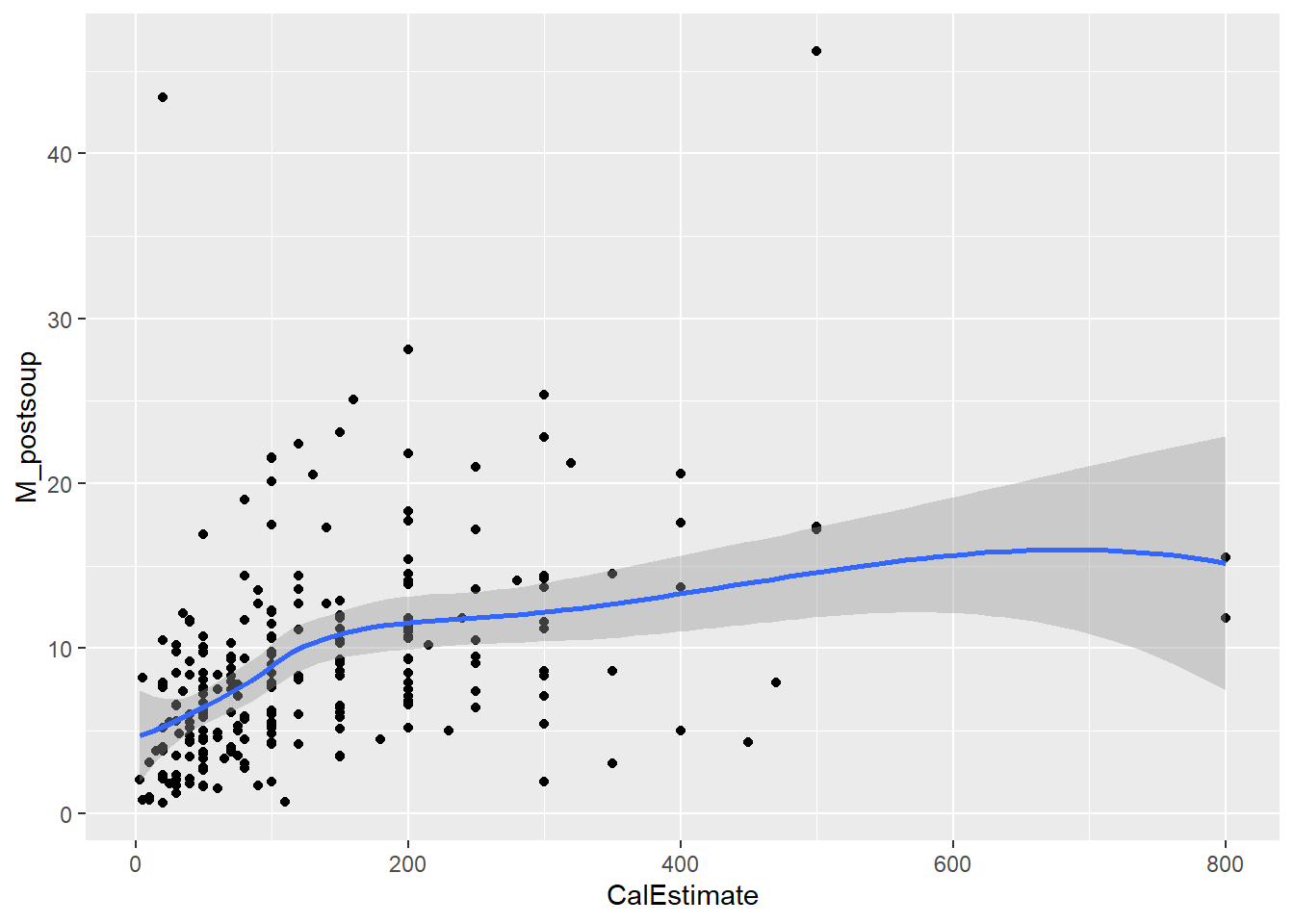
Let’s assess monotonicity with a scatterplot. Use the “loess” method to fit the curve, as we are not aiming to show a linear relationship this time.

ggplot(lopez_control_no_outliers, aes(x = CalEstimate, y = M_postsoup)) +
  geom_point() +
  geom_smooth(method = "loess")
`geom_smooth()` using formula = 'y ~ x'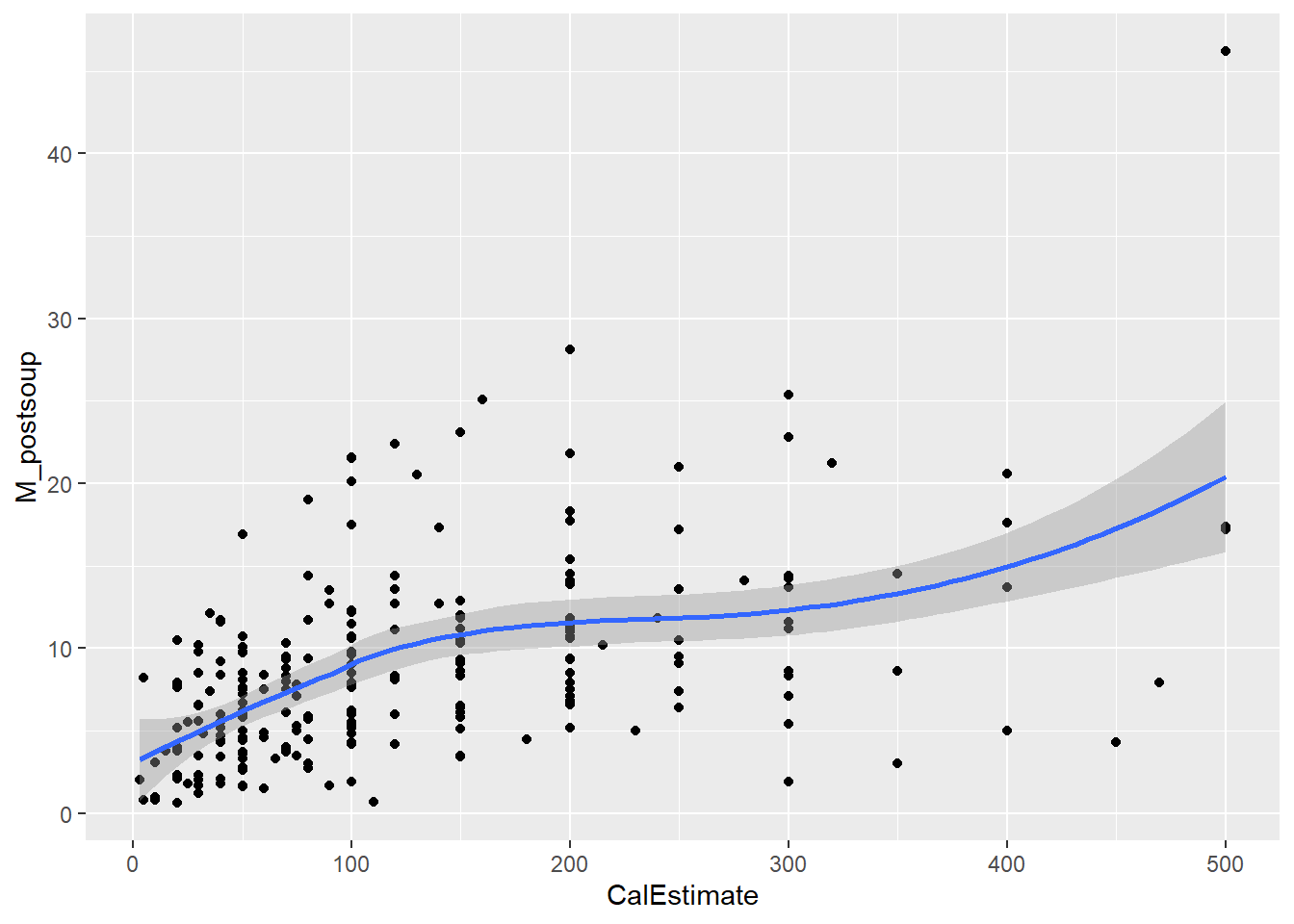

Verdict: Both assumptions hold. The line of best fit displays a clear monotonic relationship, especially with the outliers removed. Therefore, we will proceed with Spearman’s correlation.

Before proceeding, we may want to recalculate the descriptives after removing the outliers:

# descriptives for lopez_control_no_outliers
descriptives_control_no_outliers <- lopez_control_no_outliers %>% 
  summarise(n = n(),
            mean_CalEstimate = mean(CalEstimate, na.rm = TRUE),
            sd_CalEstimate = sd(CalEstimate, na.rm = TRUE),
            mean_M_postsoup = mean(M_postsoup),
            sd_M_postsoup = sd(M_postsoup)) %>% 
  ungroup()

descriptives_control_no_outliers
n mean_CalEstimate sd_CalEstimate mean_M_postsoup sd_M_postsoup
241 127.9668 105.4418 8.684232 5.862664

Next we will move on to the inferential test. The code remains the same as above, but this time we will change the method to “Spearman” and use the data object lopez_control_no_outliers.

correlation(lopez_control_no_outliers, method = "Spearman")
Parameter1 Parameter2 rho CI CI_low CI_high S p Method n_Obs
CalEstimate M_postsoup 0.5225186 0.95 0.4210739 0.6110526 1113907 0 Spearman correlation 241

Writing-up the results would be similar to the Pearson correlation above.

It was hypothesised that there would be a positive correlation between estimated calories of soup consumed \((M = 128.0 cal, SD = 105.4 cal)\) with actual consumption volume \((M = 8.68 oz, SD = 5.86 oz)\). The assumptions of linearity, normality, and homoscedasticity were assessed visually using a Residuals vs Fitted plot, a Q-Q plot, and a Scale-Location plot, respectively. These assumptions did not hold. Additionally, three outliers were removed from the dataset.

Consequently, a Spearman’s rank correlation was conducted, revealing a strong, positive, and statistically significant relationship between estimated calories of soup consumed and actual consumption volume, \(rho(239) = .522, p < .001, 95\% CI = [.421, .611]\). The study was sufficiently powered. Therefore, the null hypothesis is rejected in favour of H1.

Pair-coding

Task 1: Open the R project for the lab

Task 2: Create a new .Rmd file

… and name it something useful. If you need help, have a look at Section 1.3.

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding.

We are using the packages tidyverse and correlation today. If you have already worked through this chapter, you will have all the packages installed. If you have yet to complete Chapter 9, you will need to install the package correlation (see Section 1.5.1 for guidance if needed).

We also need to read in dog_data_clean_wide.csv. Again, I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

Task 4: Tidy data & Selecting variables of interest

Step 1: Select the variables of interest. We need 2 continuous variables today, so any of the pre- vs post-test comparison will do. I would suggest happiness ratings (i.e., SHS_pre, SHS_post). Also keep the participant id RID. Store them in a new data object called dog_happy.

Step 2: Check for missing values and remove participants with missing in either pre- or post-ratings.

Step 3: Convert participant ID into a factor

## Task 3
library(tidyverse)
library(correlation)

dog_data_wide <- read_csv("dog_data_clean_wide.csv")


## Task 4
dog_happy <- dog_data_wide %>%
  # Step 1
  select(RID, SHS_pre, SHS_post) %>% 
  # Step 2
  drop_na() %>% 
  # Step 3
  mutate(RID = factor(RID))

Task 5: Re-create the scatterplot below

`geom_smooth()` using formula = 'y ~ x'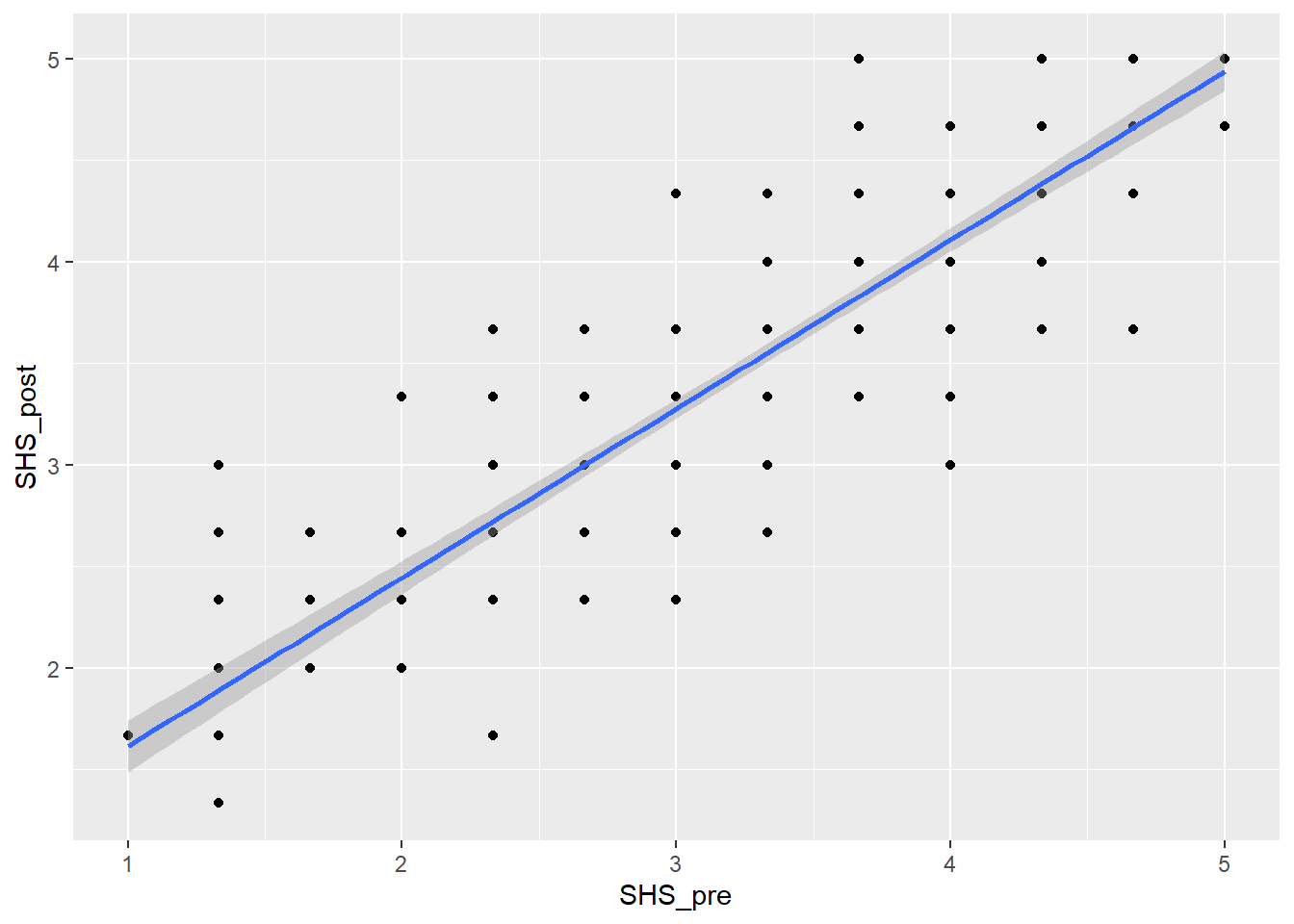

ggplot(dog_happy, aes(x = SHS_pre, y = SHS_post)) +
  geom_point() +
  geom_smooth(method = "lm")

Task 6: Assumptions check

We can either do the assumption check by looking at the scatterplot above or we can run the code plot(lm(SHS_pre~SHS_post, data = dog_happy)) and assess the assumptions there. Either way, it should give you similar responses.

  • Linearity: a relationship
  • Normality: residuals are
  • Homoscedasticity: There is
  • Outliers:

What is your conclusion from the assumptions check?

Task 6: Compute a Pearson correlation & interpret the output

  • Step 1: Compute the Pearson correlation. The structure of the function is as follows:
correlation(data = your_dataframe,
            select = "variable1",
            select2 = "variable2",
            method = "Pearson",
            alternative = "two.sided")

The default method argument is Pearson, but if you thought any of the assumptions were violated and conduct a Spearman correlation instead, change the method argument to”Spearman”.

correlation(data = dog_happy,
            select = "SHS_pre",
            select2 = "SHS_post",
            method = "Pearson",
            alternative = "two.sided")
Parameter1 Parameter2 r CI CI_low CI_high t df_error p Method n_Obs
SHS_pre SHS_post 0.8842169 0.95 0.855856 0.9072765 31.73394 281 0 Pearson correlation 283 
# alternative because there are only 2 numeric columns in `dog_happy`
correlation(dog_happy)
  • Step 2: Interpret the output

A Pearson correlation revealed a , , and statistically relationship between happiness before and after the dog intervention, r() = , p , 95% CI = [, ]. We therefore .

Important

In the write-up paragraph above, the open fields accepted answers with 2 or 3 decimal places as correct. However, in your reports, ensure that correlation values are reported with 3 decimal places.

Test your knowledge

Question 1

What is the main purpose of a Pearson correlation?

“To assess the strength and direction of a linear relationship between two continuous variables.” is the correct answer.

The other options are incorrect:

  • “To compare the means of two independent groups” is incorrect because that describes an independent t-test, not correlation.

  • “To determine the monotonic relationship between two ordinal variables” is incorrect because that describes Spearman’s correlation, not Pearson’s.

  • “To test for differences in variances between two continuous variables” is incorrect because that refers to Levene’s test or similar, not correlation.

Question 2

Which of the following is a key assumption of the Pearson correlation?

Pearson correlation assumes linearity.

The other options are incorrect:

  • “The two variables are measured on a ordinal scale” is incorrect because Pearson correlation requires interval or ratio data, but for ordinal data you would have to switch to the non-parametric equivalent (i.e. “Spearman”).

  • “The dependent variable is continuous” is incorrect because there are no dependent and independent variables in a correlation. The variables are called “measured variables” or just “variables”. And both of them need to be measured on a continuous scale.

  • “The test is robust against outliers” is incorrect because outliers can strongly influence the Pearson correlation coefficient, making it less robust in their presence.

Question 3

You perform a Pearson correlation and find \(r(244) = .415, p = .002\). How would you interpret these results??

“There is a moderate, positive, statistically significant correlation between the two variables.” is the correct answer. The correlation value (\(r=.415\)) indicates a moderate, positive relationship, and the p-value (\(p=.002\)) indicates statistical significance.

Question 4

What does a Spearman correlation coefficient of \(rho = -.729\) indicate?

“A strong, negative monotonic relationship.” is the correct answer. The value of .729 indicates a strong relationship and the minus indicates it is negative. For Spearman the relationship has to be monotonic.

The other options are incorrect:

  • “A strong, positive monotonic relationship” is incorrect because the minus implies the relationship is negative, not positive.

  • “A strong, negative linear relationship” is incorrect because Spearman measures monotonic relationships, not linear ones.

  • “A non-significant relationship” is incorrect because the question does not state the p-value or provide sample size information. Hence, we cannot assume anything about significance. For example, small samples with large rho (or r) values may not be statistically significant. Contrastingly, in large samples, smaller rho (or r) values can be significant.