Lab 3 Visualisation Through ggplot2

3.1 Overview

In the last lab we encouraged you to always be looking at your data, making sure you are understanding your data, paying attention to how it is made up in regards to data types, and what the different functions do to your data. Remember that it is one thing to get a function to run, but you need to check it is doing what you think it is doing. It is just a function. You are the human!

A second way of looking at your data, and what we are going to focus on in this chapter, is through visualisation - figures and plots - to help understand patterns and effects in your data. For example, when we asked you about the relationship between age and the Ponzo illusion in Chapter 1.

Visualisation is very important for understanding your data, for example in regards to seeing differences between groups, but also for seeing where things don't quite match up with what you think is happening. A great example of this is Anscombe's Quartet, which you can read up about at a later date if you like - see here - four datasets given exact same means but with very different underlying structures when visualised. The key point is that it is always good to visualise your data and visualisation should be a common step in your practical skill set.

In the PsyTeachR Grassroots book we introduced data visualisation using ggplot2, the main visualisation package of tidyverse. You should look back at that when working through this chapter, and you can find additional info here at the main page for the package: ggplot2.

Today we will revisit plotting data and expand your skills in order to make effective and informative figures. This will become really beneficial to you as your progress as visualisation of any data is a skill that applies to multiple careers, not just Psychology.

In this lab you will:

  1. Recap on visualisation
  2. Expand your skills to produce new figures
  3. Learn about Mental Rotation

3.2 PreClass Activity

Testing Mental Rotation Ability

The data we will use today comes from a recent replication of a classic experiment merging the fields of Perception and Cognition. Shepard and Metzler (1971) demonstrated that when participants are shown two similar three-dimensional shapes, one just a rotated version of the other (see the figure below - top panel), and asked participants whether they were the same shape or not, the reaction time and error rates of responses were a function of rotation; i.e. the larger the difference in rotation between the two shapes, the longer it took participants to say "same" or "different", and the more errors they made.

The Mental Rotation Task as shown in Ganis and Kievit (2016) Figure 1

Figure 3.1: The Mental Rotation Task as shown in Ganis and Kievit (2016) Figure 1

The image shown in Figure 3.1 actually comes from a recent replication by Ganis and Kievit (2016). In the top panel the two shapes are the same but the shape on the right is rotated vertically at 150 degrees from the original (the left shape) and so participants should respond "same". In the bottom panel however the two shapes are different; the one on the right is again rotated at 150 degrees but in this trial it takes longer for participants to realise that they are different shapes.

You can read more about Ganis and Kievit (2016) in your own time but the basic methods are that they ran 54 participants on a series of these images using 4 angles of rotation (0, 50, 100, 150 degrees) and asked people to respond same or different on each trial. The data can be downloaded from here. You should use this data to follow along below and try to answer the questions.

Visualising Data

  1. Download the data folder, unzip it, and save it to a folder you have access to (e.g. your M: drive if using the lab machines).
  2. Set your working directory to that folder Session >> Set Working Directory >> Choose Directory
  3. Open a new Rscript and save it within the folder that contains the data, giving the script a sensible name, e.g. Lab3_preclass_visualisations.R. (If you prefer to work in R Markdown like the assignments will be in then that is totally fine as well. Just remember you will need to make your own code chunks if using R Markdown, as shown in Chatper 1)
  4. Copy the three code lines below into your script and run them to bring tidyverse into the library and to read in the two datafiles.
library("tidyverse")

menrot <- read_csv("MentalRotationBehavioralData.csv")
demog <- read_csv("demographics.csv")
  • Note, there is no difference between library(tidyverse) and library("tidyverse") both will work.
  • However, there is a difference between demog <- read_csv("demographics.csv") and demog <- read_csv(demographics.csv). You will need quotes around the .csv filename as shown in the code chunk above (e.g. demog <- read_csv("demographics.csv")), or the code won't work.

This is a really great question as we always seem to be saying to use dplyr or readr or ggplot, but we never actually call them in. Remember however that tidyverse is actually a collection of packages, the most common packages in fact, and we use it to bring in these common packages (including ggplot2) because you will probably need the other packages along with it for the codes to run smoothly. We will try to tell you when you need to call other packages alongside tidyverse but do keep in mind that most of your codes will at least start with the tidyverse package.

Small point, if looking for help on ggplot, the package is actually called ggplot2. This is the newer version of the package, so search ggplot2 if you need help.


Let's start by having a look at the data we have brought in. You can do this whichever way you choose; we mentioned three ways in the previous labs - check your notes.

First, demog - short for demographics. It has three columns:

  • Participant - the ID of the participant
  • Age - the age of the participant
  • Sex - the sex of the participant

Secondly, menrot - short for mental rotation. It has 8 columns:

  • Participant - the ID of the participant; matches with ID in demog
  • Trial - the trial number in the experiment for each participant
  • Condition - the name of the image shown; R indicates the rotated image was different
  • Time - the reaction time to respond on each trial in milliseconds
  • DesiredResponse - what participants should have responded on each trial; Different or Same
  • ActualResponse - what participants did respond on each trial; Different or Same
  • Angle - the angle that the shape on the right was rotated compared to the shape on the left (0, 50, 100, 150)
  • CorrectResponse - whether the participant was correct or incorrect on a given trial

Ganis and Kievit (2016) is a very short paper that is really to introduce the stimuli set rather than give an extensive background on the topic of mental rotation - we call this a 'methods paper'. That said, the writing of the paper is very clear and the procedure is well detailed as to how they ran the actual experiment. When writing a procedure, remember to give as much information as needed to allow someone to exactly replicate your study. Have a read at this procedure when you have time and think about what information is there, but also what information is not there, to help you develop your writing and your reports. For example, which fingers did the participants use to respond and why would that be important?


Creating Some Plots

We now have our data and we want to create some plots to visualise it. We will show you the code to create four types of plots and then get you to practice some yourself, but you will remember some of this from the PsyTeachR Grassroots book. As we go through the plots, you should edit/change the code we give you and see what differences you can control and what changes you can create in the plots. Editing and altering code that works to see what happens when you change something is a great way of working. Be sure to ask any questions you have on the forums or with staff.

The two main things to know about working with ggplot are that:

  1. the usual format is:

ggplot(data, aes(x = x_axis, y = y_axis)) + geom_type_of_plot()

  1. it works on a concept of layers

On point a: The first thing you enter is your dataframe/tibble; your data. Then within the aes() you say what is my x_axis and y_axis, using the column names from within your tibble. aes stands for aesthetics and maps data into visual features. Finally you tell the code what type of plot you want.

On point b: Layers are a common way for graphics to work. Think about it as ggplot() fucntion creating your first layer and then every function after that is adding more layers on top to create the figure you want. The first layer is always your data and the axis/axes, i.e. `ggplot(....). The second layer, added by using the plus symbol '+', is the type of plot. We will look at adding more layers as we progress.

ggplot() is an incredibly powerful package that is used by a whole range of industries, including newspapers and mainstream media outlets, as it can make quite sophisticated images. One of the beauties of skills in research methods and data analysis is just how transferable they are across many fields.

3.2.1 Scatterplots - geom_point()

Scatterplots are a great way of visualising continuous data - data that can take any value on the scale it is measured. For example, in the current dataset, you can use scatterplots to explore the potential relationship between two continuous variables such as Age and Reaction Time: Do both variables increase/decrease at the same rate (i.e. a positive relationship)? Does one variable increase and the other decrease (i.e. a negative relationship)? Or maybe there is no overall relationship?

In our data, say we want to test if the overall average time to respond in the mental rotation task is related to the age of the participant. We could show this relationsthip in a scatterplotusing the code below, which:

  1. Wrangles the data to create an average response time for each participant, Mean_Time, and then joins this information to the demographic data, by Participant. All this is stored in the tibble menrot_time_age.
  2. It then plots a scatterplot (geom_point()) where age is plotted on the x axis, and Mean_Time is on the y axis
  3. Finally, it uses an additional aes call to color by Sex which will color each point based on whether it was a male or female participant responding. This is the default coloring of this call when there are two options. Later we will look at controlling this and using more colors ourselves.
menrot_time_age <- group_by(menrot, Participant) %>% 
  summarise(Mean_Time = mean(Time, na.rm = TRUE)) %>%
  inner_join(demog, "Participant")

ggplot(data = menrot_time_age, 
       aes(x = Age, 
           y = Mean_Time, 
           color = Sex)) +
  geom_point()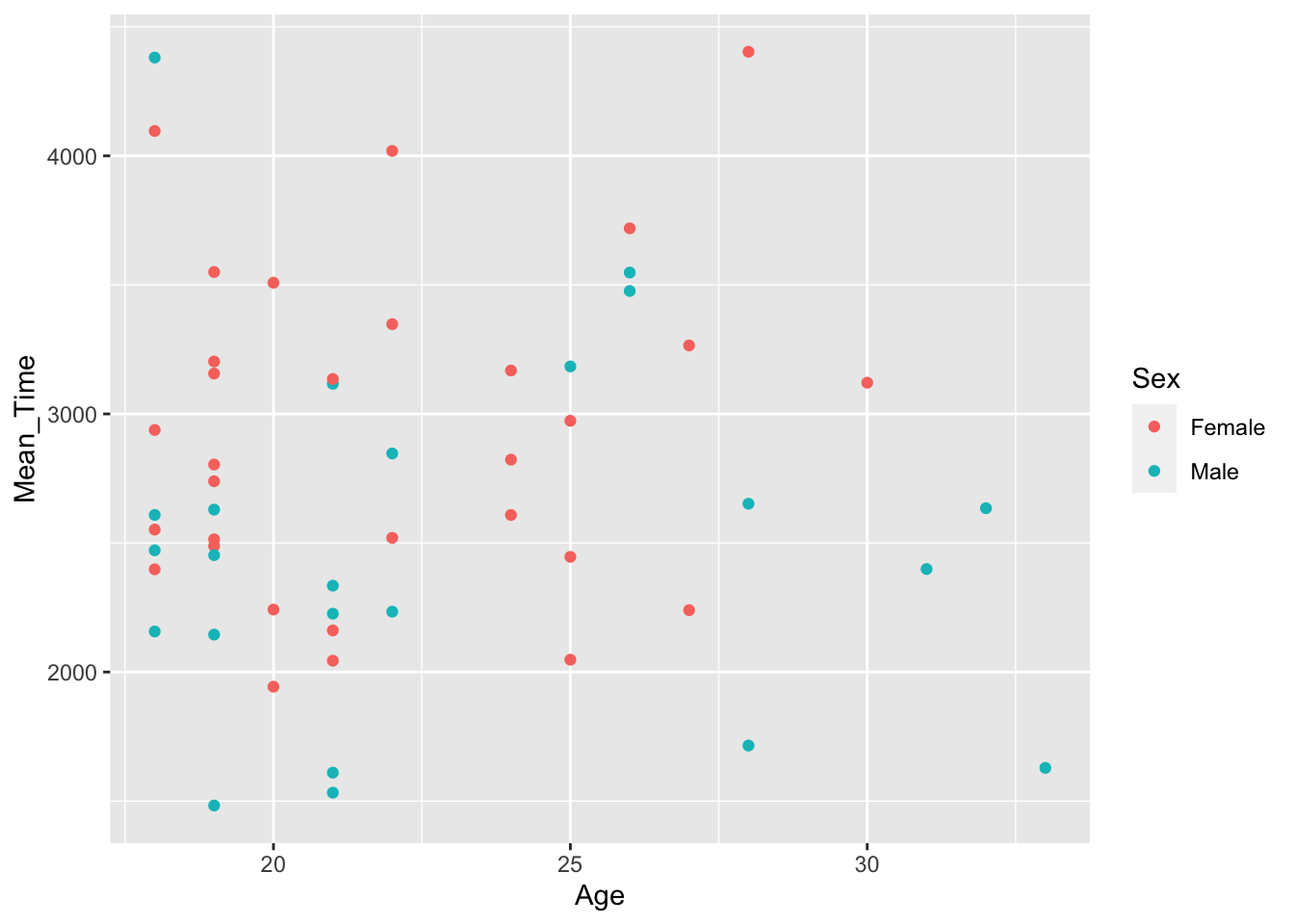
A scatterplot of Mean Time as a function of Age

Figure 3.2: A scatterplot of Mean Time as a function of Age

Quickfire Questions

  • Looking at the scatterplot in Figure 3.2, what can you say about the relationship between age and overall response time?

  • Looking at the scatterplot, what can you say about difference between male and female participants?

If you look at the figure, does it appear that as age increases (x axis) so does overall resposne time (y axis)? Or as age decreases so does overall response time? Or maybe even as age increases, overall response time decreases? Etc etc. Well, actually, looking at the figure there appears to be no relationship between the two variables at all and it is not the case that as one either increases or decreases so does the other. The relationship appears flat.

When comparing sex, based on the color of the dots, again there appears to be no major differences here as the relationship looks flat for both sex.

Later in the book we will look at correlational analysis - a method of quantifying the relationship between two variables.


Note: It will often be the case that to visualise data you first have to wrangle it into a format. When we do this we will be using the functions we saw in Chapter 2, so make sure you have been through those tasks and have understood what the wrangle verbs are doing and how pipes work. Keep in mind that most functions use the format, function(data, argument)

3.2.2 Histograms - geom_histogram()

Histograms are a great way of showing the overall distribution of your data. Does your data look normally distributed? Or is your data skewed - positive skew or negative skew? Is it peaky? Is it flat? These are terms that will become familiar to you as you learn more about statistics, so try to think about these terms and concepts when visualising, and looking at, your data.

Looking at our data, say we wanted to test if the overall distribution of mean response times for correct trials was normally distributed. We could visualise this question through the following code, which:

  1. Wrangles the data to create an average response time for each participant, Mean_Time, and then filters this information for correct trials only. This is then stored in the tibble menrot_hist_correct
  2. Plots a histogram (geom_histogram()) where Mean_Time is plotted on the x axis, and the count of each value in Mean_Time is plotted on the y axis. The code creates the y axis automatically and we don't have to state it:
menrot_hist_correct <- group_by(menrot, Participant, CorrectResponse) %>% 
  summarise(Mean_Time = mean(Time, na.rm = TRUE)) %>%
  filter(CorrectResponse == "Correct")

ggplot(data = menrot_hist_correct, 
       aes(x = Mean_Time)) + 
  geom_histogram()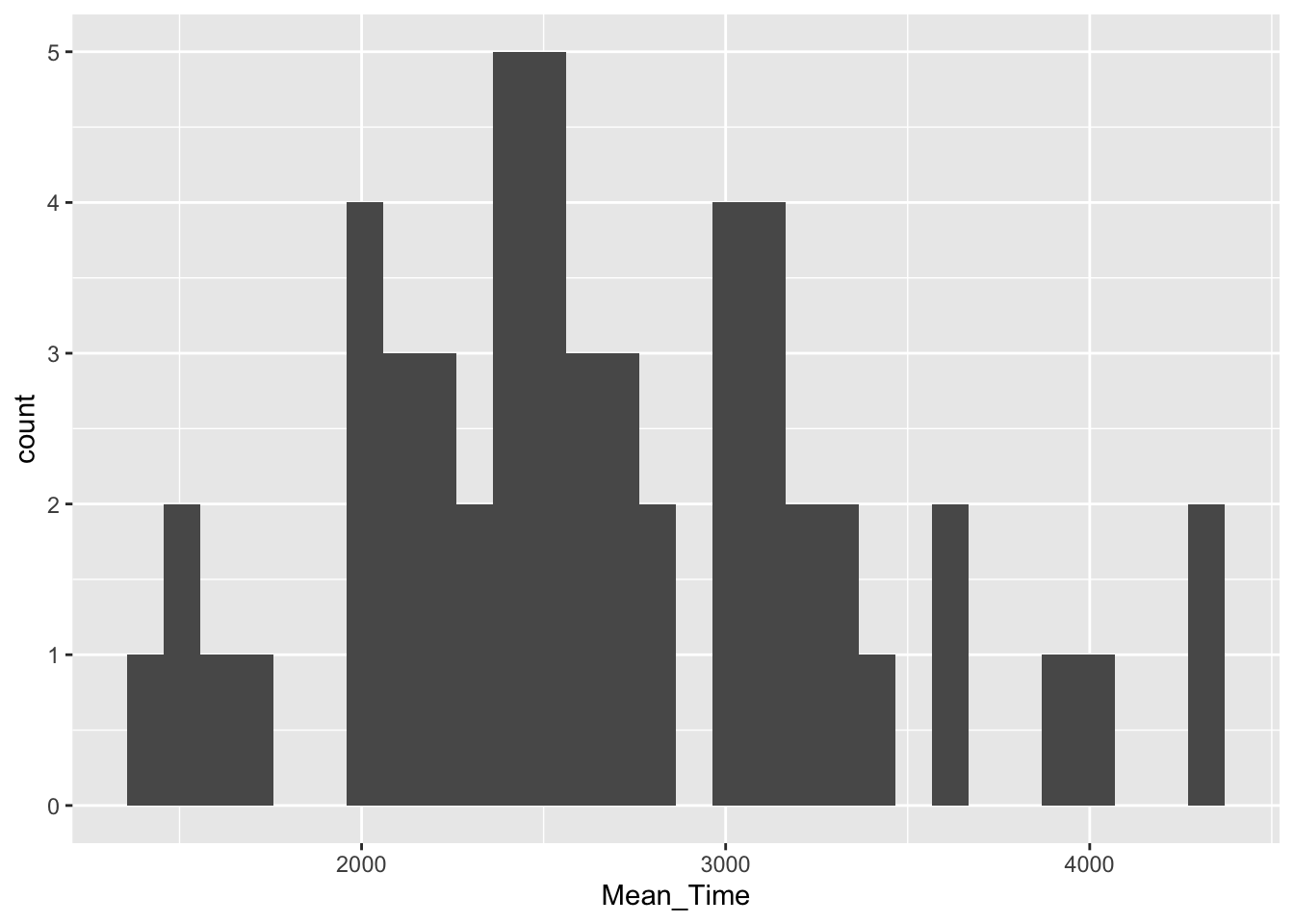
A histogram of distribution of Mean Time counts

Figure 3.3: A histogram of distribution of Mean Time counts

Quickfire Questions

  • Looking at the histogram in Figure 3.3, what can you say about the overall shape of the distribution?

  • Looking at the histogram, what is the most common average overall response time for correct trials?

Keep in mind that real data will never give that beautiful textbook shape that you see in classic diagrams when looking for normally distributed data or skewed data. Your decisions regarding your distributions will often requre a degree of judgement.

From your lectures you will remember that positive skewed data means that most of the data is shifted to the left (low numbers) with a tail stretching to the right (high numbers). Negative skew is where most of the data is shifted to the right (high numbers) with a tail stretching to the left (low numbers). Normally distributed data has most of the data in the middle with even tails on either side. Although not perfect, the data shown in our histogram is a reasonable representation of normally distributed data in the real world; particularly for a small sample of participants.

As the y axis is the count of the values on the x axis, the most common overall response time can be found by reading the highest column of the data. For this distribution, this looks to be around 2500 milliseconds or 2.5 seconds.

3.2.3 Boxplots - geom_boxplot()

Boxplots are a great means for visualising the spread of your data and for highlighting outliers in your data. When looking at boxplots, you should consider:

  • whether the median (thick horizontal black line) is in the middle of its box or is higher or lower than the middle of the box?
  • whether the box is evenly disributed round the median or not?
  • are the box whiskers (vertical tails at top and bottom of box) a similar length on both sides of the box?
  • are there any outliers - usually highlighted as a star or a dot beyond the whiskers?

Using today's data, let's look at and compare the distributions of mean reaction times for correct and incorrect responses. This can be done using the below code, which:

  1. Repeats the first two wrangle steps as when we created a scatterplot, but additionally groups by CorrectResponse, and stores the data in the tibble menrot_box_correct
  2. Plots a boxplot (geom_boxplot()) of the overall average response times on the y-axis, Mean_Time, based on the condition, CorrectResponse, on the x-axis
  3. Uses an additional aes call to fill the colour of the boxplots, of the two categories, based on whether CorrectResponse was correct or incorrect. Again these are default and we will look at editing this later.
  4. Turns off the legend using the guides() call as it isn't needed because the x-axis tells you which group is which. More on that later though. Run the code as is. Now run the code with fill = TRUE instead. What's the difference? Notice that fill is the name of the call in the ggpot(...) function. They are linked.
menrot_box_correct <- group_by(menrot, Participant, CorrectResponse) %>% 
  summarise(Mean_Time = mean(Time, na.rm = TRUE)) %>%
  inner_join(demog, "Participant")

ggplot(data = menrot_box_correct, 
       aes(x = CorrectResponse, 
           y = Mean_Time, 
           fill = CorrectResponse)) + 
  geom_boxplot() +
  guides(fill = FALSE)
## `summarise()` has grouped output by 'Participant'. You can override using the `.groups` argument.
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.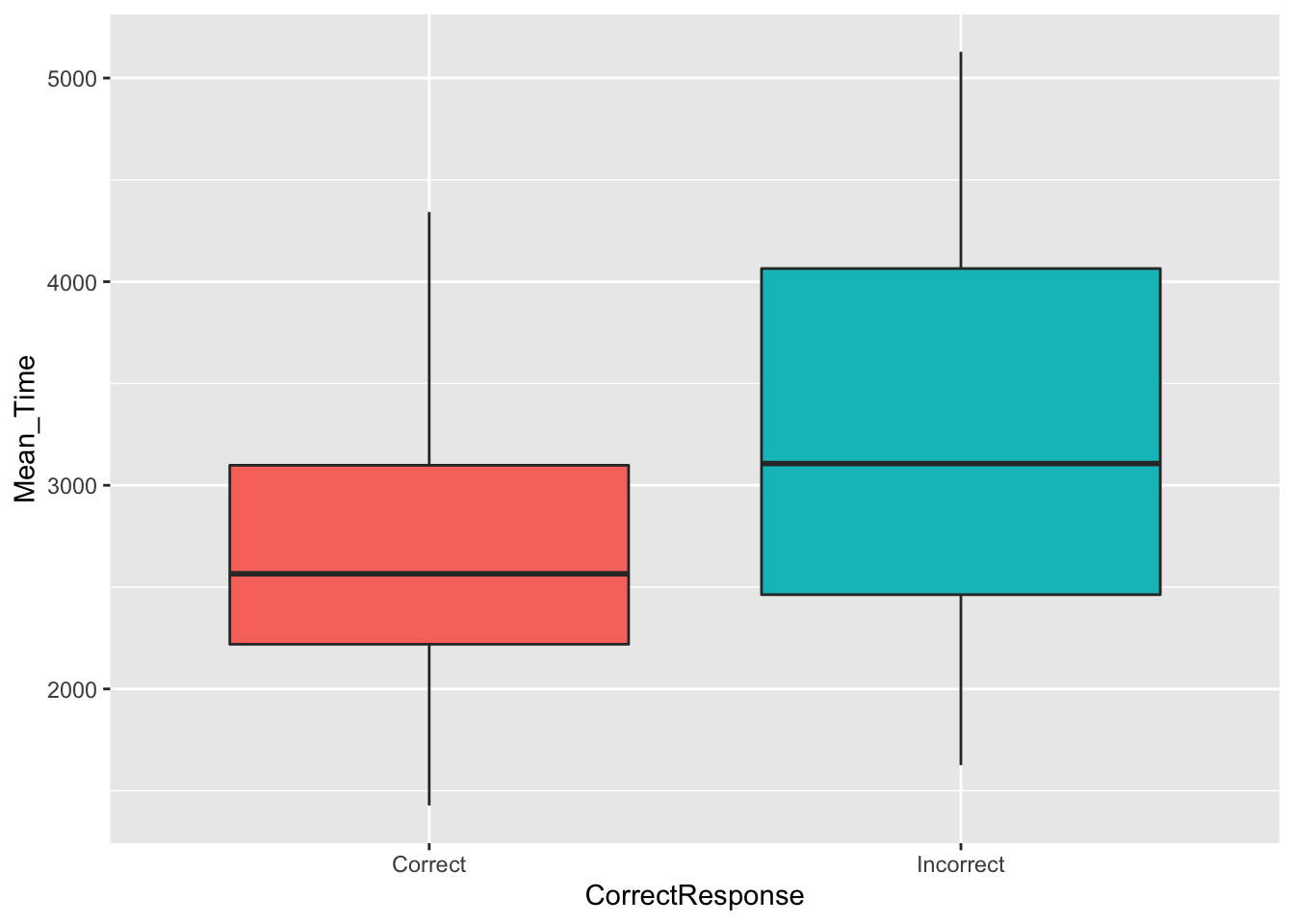
A boxplot of the spreads of Mean Time for Correct and Incorrect Responses

Figure 3.4: A boxplot of the spreads of Mean Time for Correct and Incorrect Responses

Quickfire Questions

  • Looking at the boxplots, how many outliers were there?

  • Looking at the boxplots in Figure 3.4, which condition has the longer median overall average response time to the mental rotation task?

There are a number of ways of determining outliers which will be discussed in more detail when you learn about statistics. Two methods are through standard deviations (usually 2.5 or 3 SD are used as cut-offs) or through boxplots, where an outlier is determined as \(1.5*IQR\) (inter-quartile range) above or below the top and bottom of the box. Outliers are shown as dots above or below the whiskers of the boxplot. As you can see in the figure there are no outliers to see in this data.

The median is one of the 5 values required to make a boxplot and is shown as the horizontal thick black line within the box itself. Looking at the two conditions and comparing the position of the median on the y axis (response time) we can see that the median response time for incorrect trials was higher than correct trials. This would suggest that people take longer to make up their mind and to give a decision on the trials that they get wrong. Makes sense if you think about it; uncertainty takes longer and leads to more errors.

3.2.4 Barplots - geom_bar() or geom_col()

Barplots typically show specific values of a condition. Sometimes this will be really simple like the count of a variable the mean, e.g. how many people replied yes. Others will show something a bit more complex such as the average spread of values via error bars, e.g. standard error. When looking at barplots, the main considerations are whether or not there appears to be a difference between the conditions you are interested in or are all conditions about the same? It is worth knowing that barplots are now used less frequently than they were as they actually do not show a lot of information, as discussed in this blog, One simple step to improving statistical inference. However, you will still see them being used so it is great to be able to create and interpret them.

Using geom_bar()

Using our data, let's say we are interested in whether there is a difference in the average percentage of correct and incorrect responses across male and female participants. We could visualise this using the following code, which:

  1. Wrangles the data through a series of steps to establish the overall percent average for correct and incorrect responses for both sex, stored in menrot_resp_sex.
  2. Plots a barplot (geom_bar()) with the condition Sex on the x axis, the Avg_Percent on the y axis, created through the wrangle, and fill the bars based on CorrectResponse
  3. Finally, within the geom_bar it says to treat the data as final values and not to average them, stat = "identity", and makes both columns visible by moving them apart position = position_dodge(.9)) - without this last step the bars would overlap and you wouldn't see everything. Try changing the .9
  • Note: Each participant did 96 trials in this study.
total_n_trials <- 96

menrot_resp_sex <- count(menrot, Participant, CorrectResponse) %>% 
  inner_join(demog, "Participant") %>%
  mutate(PercentPerParticipant = (n/total_n_trials)*100) %>%
  group_by(Sex, CorrectResponse) %>%
  summarise(Avg_Percent = mean(PercentPerParticipant))

ggplot(data = menrot_resp_sex, 
       aes(x = Sex, 
           y = Avg_Percent, 
           fill = CorrectResponse)) + 
  geom_bar(stat = "identity", 
           position = position_dodge(.9))
## `summarise()` has grouped output by 'Sex'. You can override using the `.groups` argument.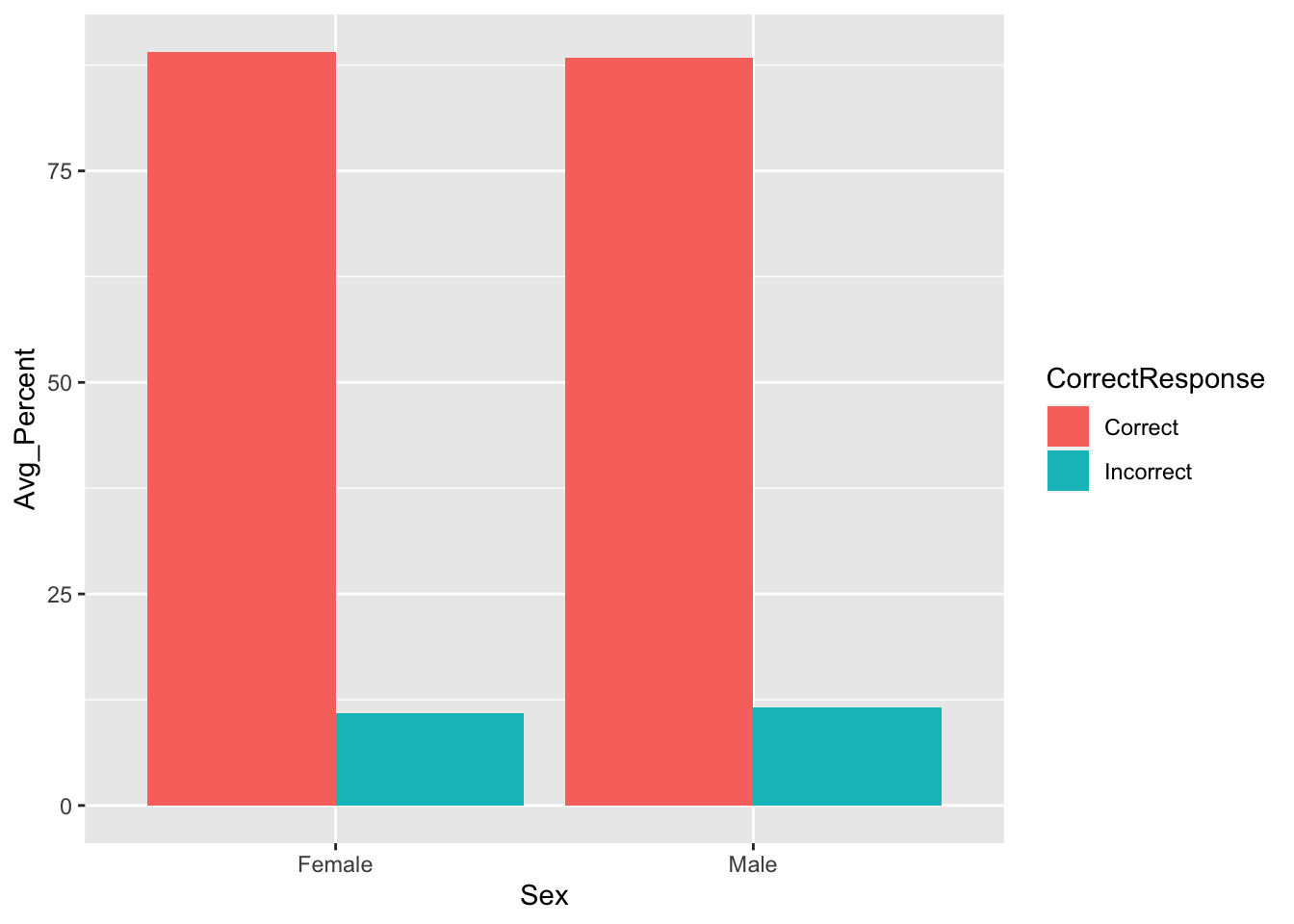
A barplot of the average percent Correct and Incorrect responses for Female and Male participants - using geom_bar()

Figure 3.5: A barplot of the average percent Correct and Incorrect responses for Female and Male participants - using geom_bar()


Using geom_col()

geom_col() - short for column - is an alternative to geom_bar() that does not require the part of the code where you say to not do anything to the data, i.e. stat="identity". This is shown below. Notice the difference in codes but that they produce the same figure!

ggplot(data = menrot_resp_sex, 
       aes(x = Sex, 
           y = Avg_Percent, 
           fill = CorrectResponse)) +
  geom_col(position = position_dodge(.9))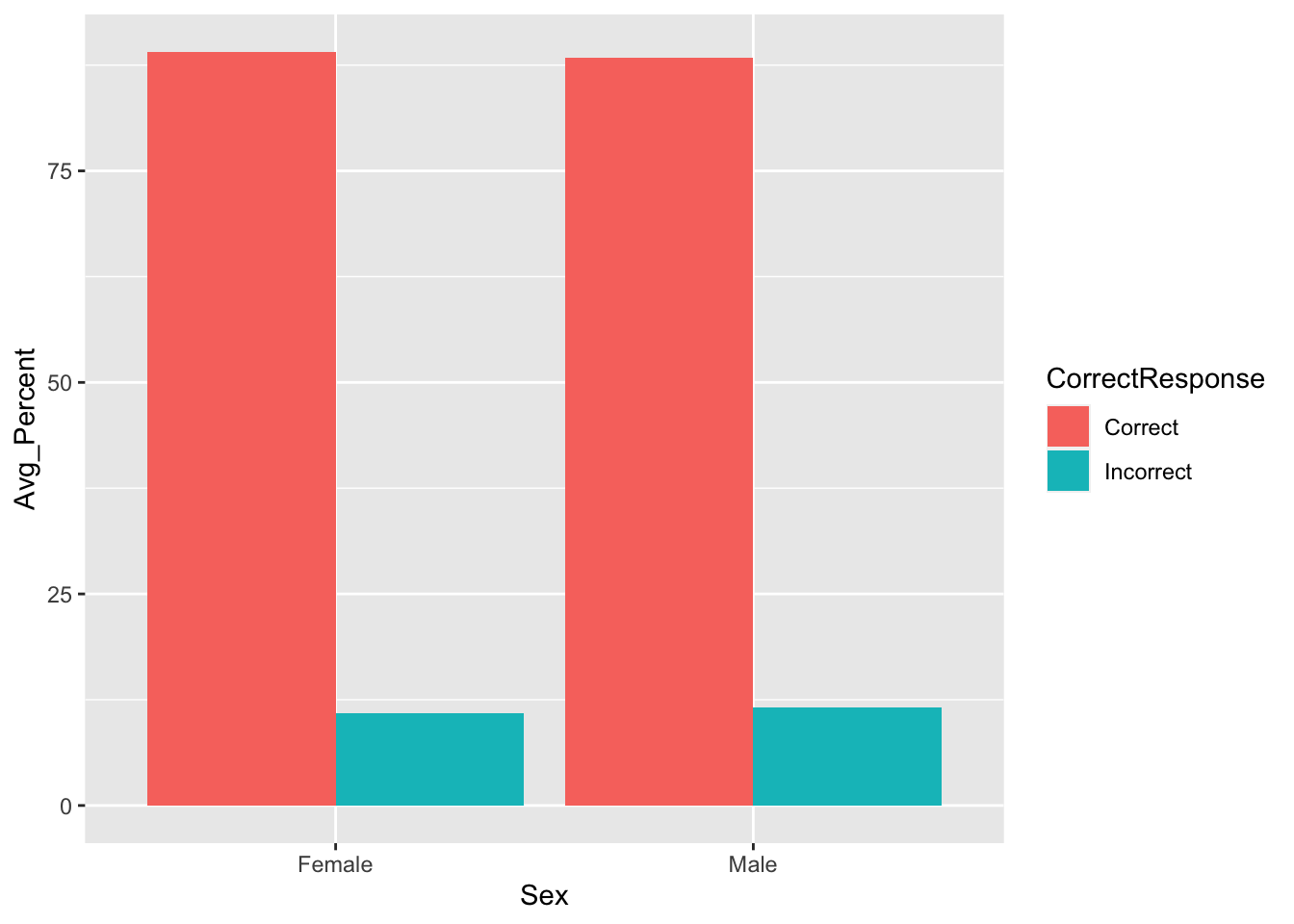
A barplot of the average percent Correct and Incorrect responses for Female and Male participants - using geom_col()

Figure 3.6: A barplot of the average percent Correct and Incorrect responses for Female and Male participants - using geom_col()

Quickfire Questions

  • Looking at the barplot and data, on average, which sex had the most correct responses?

  • Looking at the barplot and data, on average, which sex had the most incorrect responses?

  • Looking at the code, what happens if you decrease the position.dodge() value?

  • Looking at the code, what happens if you change the aes call of fill to color?

Remember that in barplots plotting the mean, the top of the column is the average value of that condition. This is actually why people do not like barplots; though commonly used, they really only show you one value for your data, the average, and they disregard all other information unless some indication of spread is given.

With that in mind, comparing the two Correct columns we can see that females had on average more correct responses than males. Doing the same for the Incorrect columns we can see that males had more incorrect responses than females. This actually makes sense as the response option in the experiment was either correct or incorrect, so when you add all the correct and incorrect percentage responses for one sex together you should get 100%. If females gave more correct reponses then they must have given less incorrect responses.

The last two questions are about playing with the code. Remember we said that plots work through a concept of layers. If you set position.dodge() to 0, you will find that one of the columns disappears because they completely overlap now. So we need to set position.dodge() to a reasonable value to have the columns separate. Why not set it at 1? In barplots you often find that the different levels (or categories) of the the same variable are touching. Note however that the value of the dodge, in this case 1, is relative to the size of the x axis - if the scale of your x-axis ran from 0 to 100 then a dodge of 1 will have very little effect. Sometimes you need a little trial and error. Always look at the output of your code.

The final point shows that you can add a lot more calls than just x and y axis to change the presentation of your figures. fill changes the color of the columns, color changes the outline color of the columns. We will see more of these as we progress and we will look at the difference between putting them inside the aes() and outside of it. Have a play about with these on other figures and see what happens. It is worth pointing out here though, above where we turned the legend off using guides(fill = FALSE), that works because we used the fill = ... call to change colours. If we had used the color = ... call to change colours we need to use guides(colors = FALSE) to turn off the legend. See how they are linked? The guide matches what you called.

3.2.5 Themes, Labels, Guides, and facet_wraps()

Before we finish, we want to mention a couple of other layers you can add to your ggplot calls to make your figures look more professional. We will show you the code here but we want you to run them and teach yourself how they work by changing the code, removing parts within ggplot, and by adding them to the other figures we have shown above. Ask any questions you have about these functions on the forums or check them with a member of staff.

  • themes - changing the overall presentation of your figure. Try running the below code and comparing the figure to the barplot above. Remember, ?theme_bw() will give some information or look at the cheatsheets for different themes such as theme_light(), theme_classic(), theme_gray() and theme_dark().

    • theme_gray() is actually the default and is equivalent to not stating any theme function. _ theme_classic() is very close to a basic APA figure presentation.

  • labs - putting appropriate labels on your figures so readers understand what is being displayed. Try changing the text within the quotes.

  • facet_wraps - splitting data into separate figures for clarity. This will only work when one of your conditions is categorical but it can be a really effective means of displaying information.

  • guides - remove it and see what happens. Do you understand why we use fill in this situation but perhaps not others?

Try running and editing this code.

total_n_trials <- 96

menrot_better_plot <- count(menrot, Participant, CorrectResponse) %>% 
  inner_join(demog, "Participant") %>%
  mutate(PercentPerParticipant = n/total_n_trials) %>%
  group_by(Sex, CorrectResponse) %>%
  summarise(Avg_Percent = mean(PercentPerParticipant))

ggplot(data = menrot_better_plot, 
       aes(x = Sex,
           y = Avg_Percent, 
           fill = CorrectResponse)) + 
  geom_col(position = position_dodge(.9)) +
  labs(x = "Sex of Participant", 
       y = "Percent Average (%)") +
  guides(fill = FALSE) +
  facet_wrap(~CorrectResponse) +
  theme_bw()

A figure for all occasions

As you progress through Psychology you will come across a variety of different figures and plots, each looking slightly different and giving different information. When looking at these figures, and indeed when choosing one for your own analyses, you have to think about which figure is the most appropriate for your data. For example, scatterplots are great when both variables are continuous; boxplots and histograms are great for viewing spreads of data; barplots are commonly used where one variable is categorical - but as above note that barplots can be misleading and lots of new approaches to display categorical information are being created. Always keep asking yourself, does my plot display my data correctly. Also, do I have the right number of dots/conditions/groups in my figure? Too many or too few would suggest something is not quite right. Look at your data!

Job Done - Activity Complete!

We will look more figures and controlling different aspects of them in the coming chapters. We will also look at interpreting the figures. The skill of interpretation is of course more important than what color to show them in. But changing colors is fun and a good way to learn how to work with the codes!

If you have any questions please post them on the available forums or check with a member of staff. Finally, don't forget to add any useful information to your Portfolio before you leave it too long and forget.

3.3 InClass Activity

Mental Rotation and Visualisations

Visualisation is a key part of data analysis in exploring data, checking assumptions, and displaying results. Also, it is a really important skill for when you want to share your findings with others. As you develop your skills in Psychology you will start to analyse your own datasets, and learning how best to plot in different ways will benefit you in the long run. Keep in mind that this is a skill that you can carry into your future career even if that is outside of science.

For visualisaion we use ggplot2 and below we have listed some great online resources that you might want to consult if you want a fuller understanding.

But don't forget about what you have already covered in the PsyTeachR Grassroots book. It is highly recommended that you consult the ggplot2 cheatsheet when you work with the package to get familiar with the package.

3.3.1 Mental Rotation: Angle and Reaction Time

We will use the same dataset for this class as we did in the preclass activity. To recap, Ganis and Kievit (2016) created a modern stimuli set to test the classic experiment on mental rotation first proposed by Shepard and Metzler (1971). The idea is that the more rotated a test image is from an original image, the longer it will take for participants to determine if they are the same image or if they are completely different images. Results show that this is the case and suggest that, when doing mental rotation tasks, people do a form of internal linear interpolation, or internal mental rotation, meaning that they rotate the image in their mind back to the original angle and then compare the two images. This would be opposed to a more rapid contrast and compare approach not involving any rotation. As a result, the more rotation an image needs, the longer the task takes.

Ganis and Kievit ran 54 participants on a series of these rotated images using 4 angles of rotation (0, 50, 100, 150 degrees rotated compared to the original) and asked people to respond 'same' or 'different' on each trial. Today, to further your understanding of this experiment as well as develop your skills in visualisation and interpretation, we will look at mean reaction time for correct trials, as a function of the angle of rotation and sex. The data can be downloaded from here.

You will come across this phrase 'as a function of' quite a bit when dealing with visualisations. It means something like 'compared by' or 'across'. So you could say we are going to look at Mean Reaction Time across the four different Angles of Rotation which would be written as Mean Reaction Time as a function of Angle of Rotation. Usually it would be plotted as y axis as a function of x axis. It is a similar idea to the functions we use in our codes in that you want to see what happens when you put y in the function x. It is good to become familiar with the terms and language that is used in reports so that a) you understand what you are reading and b) you can use the same language in your writing to give a professional feel.

Remember to be developing your own notes as you go!

3.3.2 Task 1: Loading and Viewing the Data

  1. Download the data, unzip it, and save it to a folder you have access to - e.g. somewhere on your M: drive
  2. Set your working directory to the folder with your data in it. Do this through the menus at the top of RStudio, not through code.
  3. Start a new script, save it to the folder with your data in it. Again R script or R Markdown will both be fine. Your choice.
  4. In your script, load in the tidyverse library.
  5. Load in both datasets exactly as we did in the preclass, storing the experimental data in menrot and the demographic data in demog.

library()

menrot <- read_csv()

demog <- read_csv()


Remember to always be looking at your data as good practice and to make sure it is as you expect it to be. Use either View() or glimpse() but do this in the console window of RStudio, never in your script or .Rmd file. Other useful functions that you can use to check your data structure are:

  1. str() - This shows what type your data is. Look for words like table, dataframe, character, integer, double.
  2. head(), tail(), and names() - These show the top six and bottom six rows with column names, or just the column names with names().
  3. dim() - This shows the dimensions of the data.

Refer to the preclass for a list of what all the columns refer to if you are not sure. And keep in mind that to be reproducible means being careful with the spelling and punctuation of the names of functions, tibbles, columns, conditions, etc, at all times - e.g. Juggler is not the same as juggler.

Quickfire Questions

Take a couple of minutes to try the above functions and to answer the following questions.

  • From the options, what type of data is the variable Angle, found in the dataframe menrot?

  • Type in the box the name of the dataframe that contains information regarding the sex of the participants:

  • From the options, which of these is a column within menrot?

  • From the options, according to the dim() call, how many rows are there in demog?

This is about making sure you are loading in your data correctly, using the instructed names - so that you are being reproducible - and that you understand the data you are looking at. If you completed Task 1 successfully, loading in the data to the correct dataframes, then the following answers should work in the above questions.

  1. calling str(menrot) and looking through the information that comes out you should see that the data in the column Angle are loaded in as double/numerical. Technically they are integers (whole numbers with no decimal places) but the default load in would make them numerical.

  2. demog should have been where you loaded information regarding the demographics including sex of participant.

  3. names(menrot) will give you column names. This question is about making sure of the correct spelling: CorrectResponse. All the other spellings would not work in this data as spelling of column names is specific!

  4. dim(demog) shows you the number of rows (54) by the number of columns (3).

3.3.3 Task 2: Recreating the Figure

Let's start by making a representation of the top part of Figure 2 in Ganis and Kievit (2016) - Mean Reaction Time as a function of Angle of Rotation.

  1. Copy the lines of code below into your script.

  2. Replace the NULLs in order to recreate the figure below similar to that of Ganis and Kievit (2016) Figure 2 (top).

    • Note that this figure shows information for only correct responses just as in Ganis and Kievit (2016).
    • Remember ggplot is a case of layers. The first layer says where is my data and what do I want on each axis. Every subsequent layer says how I want the data displayed - points (geom_point()) with a connecting line (geom_line()).
    • After running through all these tasks, come back to this one and see if you can figure out what coord_cartesian() does by changing the numbers in the ylim = () call. There is a comment on this in the solutions.
menrot_angle <- filter(menrot, CorrectResponse == NULL) %>%
  inner_join(demog, NULL) %>%
  group_by(NULL) %>% 
  summarise(mean_Resp = mean(NULL))

ggplot(data = NULL, aes(x = NULL, y = NULL)) + 
  geom_point() +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)

The first four lines, to create menrot_angle, are all functions from the Wickham Six verbs so refer back to your portfolio to see how they work.

  1. Which answer in CorrectResponse would allow you to keep just the correct answers?

  2. What common variable will allow you to join this information to demog?

  3. You only really care about the four levels of rotation, so what variable/column will you group_by?

  4. Which variable/column do you want the mean of for a mean response time?

For the ggplot line, think of the format, data, then the x axis name, then the y axis name. See your portfolio for examples.


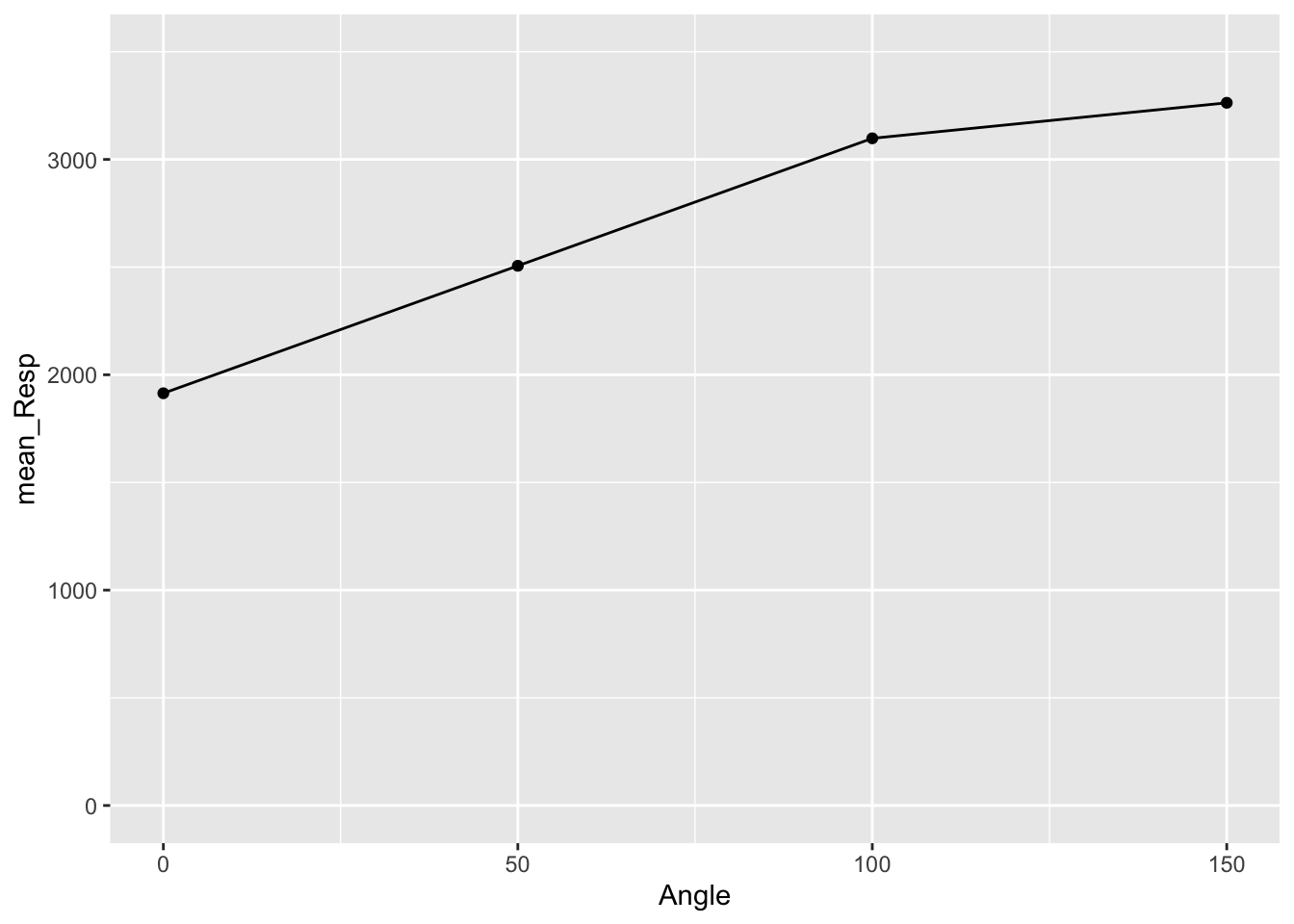
Basic Scatterplot of Response Time by Angle of Rotation

Figure 3.7: Basic Scatterplot of Response Time by Angle of Rotation

Group Discussion Point

Great, you have replicated the figure! However, do you know what it means? Spend a couple of minutes discussing with your partner or group - what does the figure tell you about mean reaction time and angle of rotation, and how does it fit with the overall theory we introduced above? Answering this question may help:

  • From the options, the figure would suggest that as angle of rotation increases:

As you can see from the figure, consistent with Shepard and Metzler (1971), the participants from Ganis and Kievit (2016) showed an increase in reaction time as the angle of rotation increased. Therefore, Ganis and Kievit (2016) have replicated the findings of Shepard and Metzler (1971).

A quick note though is that, yes, mean reaction time does increase with angle of rotation but it is not a consistent increase. You will see that the difference between mean reaction times for 150 and 100 degrees is smaller than between 0 and 50. Reaction times start to plateau after a certain angle of rotation.

3.3.4 Task 3: Examining Additional Variable Effects

In the preclass, we looked at sex of participant a lot and that was quite interesting. It is not covered in Ganis and Kievit (2016) so let us take a look at it for them.

  1. To your pipeline of Task 2, add the variable Sex to the group_by() function to group the data by Angle and Sex.
  2. Running the code again creates the below figure.

group_by(Angle, Sex)

Remember, to add more grouping variables just separate them by a comma. Everything else in our code stays the same. 


## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.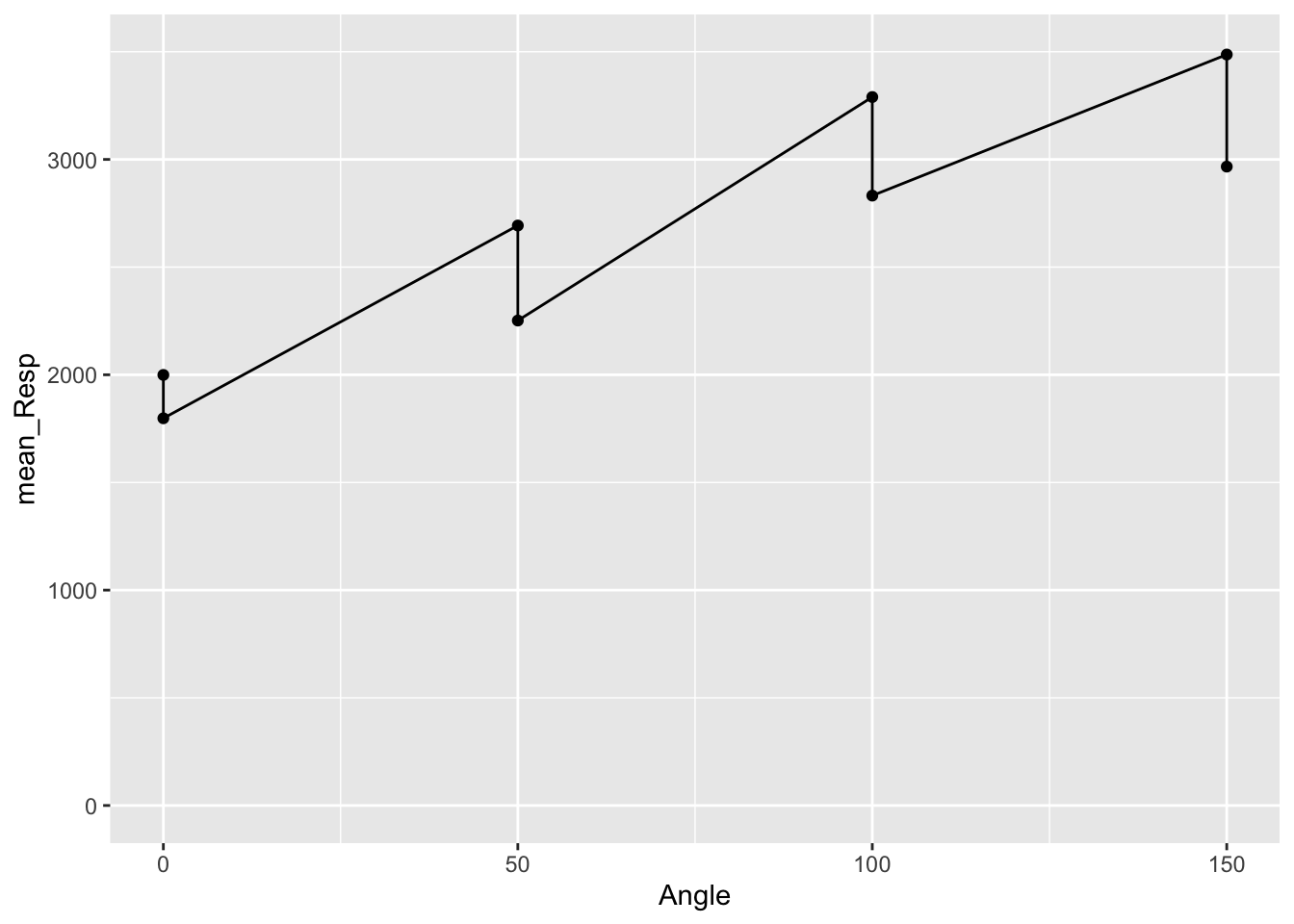
Separating points by Sex

Figure 3.8: Separating points by Sex

Hmmm, that figure does not look that informative. It looks similar to the one we created but the dots have doubled - we now have 8 instead of 4 - but we do not know which is male or female, and the connecting line is confusing. We need to add a little more to the code to tell it how to separate the data based on sex.

3.3.5 Task 4: Grouping the Figure Data

  1. In the preclass we used fill and color inside the aes() to change basic information about the figure. There is also one called group. Add a group call inside your aes(...) to separate the data by Sex.
  2. Run the code again and see what your figure looks like

ggplot(....., aes(x = , y = , group = ???))


You should now at least see different lines for the two sex, but we still can't tell which sex is which line, can we? It just looks like two black parallel lines, one slightly higher than the other. What would be ideal would be changing the color of the points based on whether they are from male or female participants! Fortunately, the geoms can also take information as well.

3.3.6 Task 5: Identifying Groups Using aes()

  1. Add an aes() call inside your geom_point() function to color the dots by Sex.

geom_point(aes(??? = ???)


You should now have something like this: 

## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.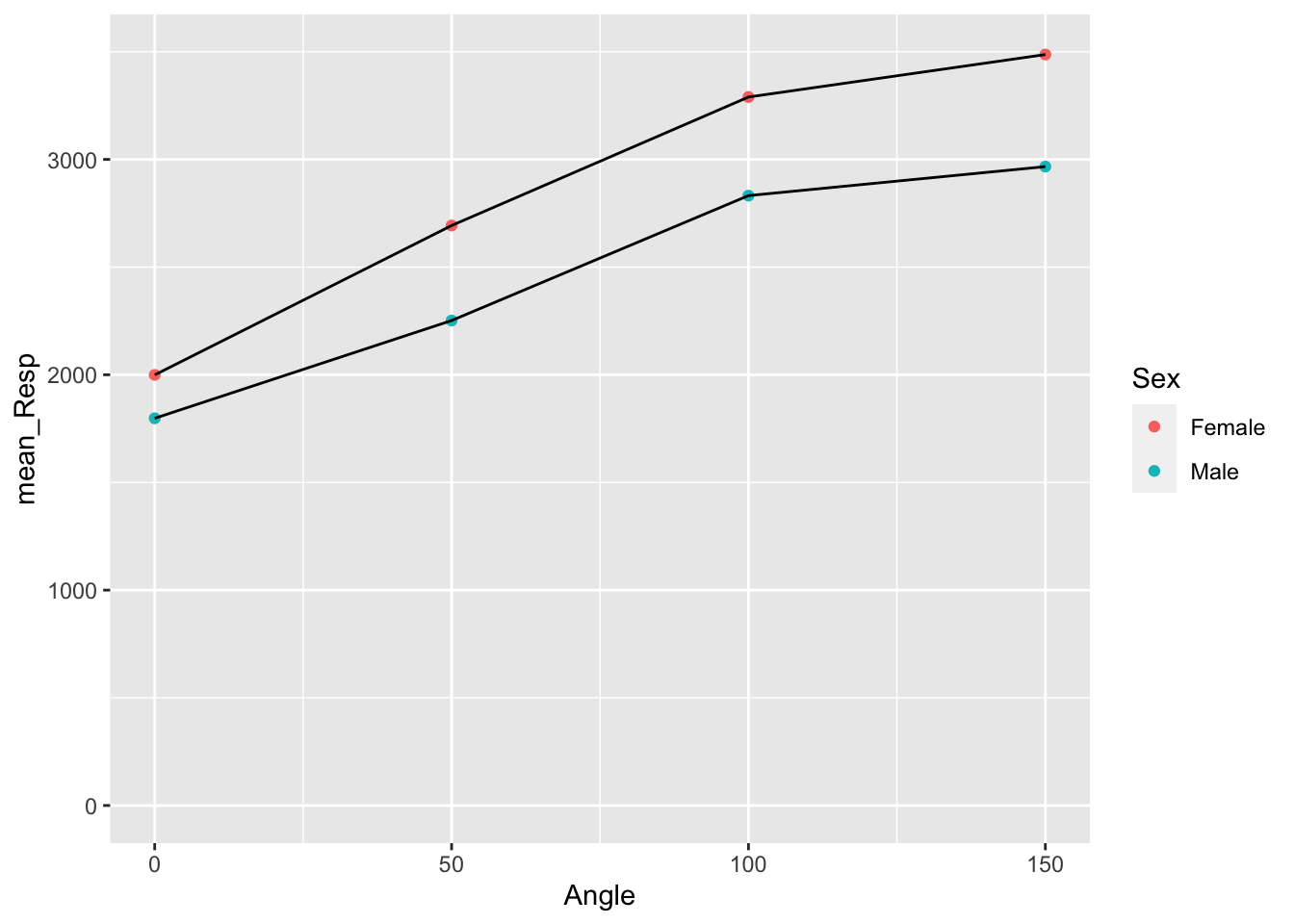
Separate lines for each Sex

Figure 3.9: Separate lines for each Sex

Great! We can now see that the female line is on top and the male line is on the bottom. But before we start interpreting this figure let's finish tidying it up with a few more tasks. For example the dots for each data point are perhaps a little small for our old eyes to see, so we could increase them in size. Also, color is great if you can print in color but we could also change the shape of the dots to help people distinguish between the Sex for when displaying in color isn't an option. To do this we will use the additional calls of shape and size within our geom_point().

3.3.7 Task 6: Changing the Shape and Size of Data Points

  1. We want each Sex to have different shaped points, so add a call to shape within the aes() call of our geom_point() function, just like you did for color.

  2. However, we want each Sex to have the same size of point, so add a call to size within the geom_point() function, but not inside the aes() call. Set an appropriate number for the size instead of naming a variable. Maybe size = 3?

geom_point(aes(color = Sex, Shape = ???), size = ???)


This should give you a figure like this:

## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.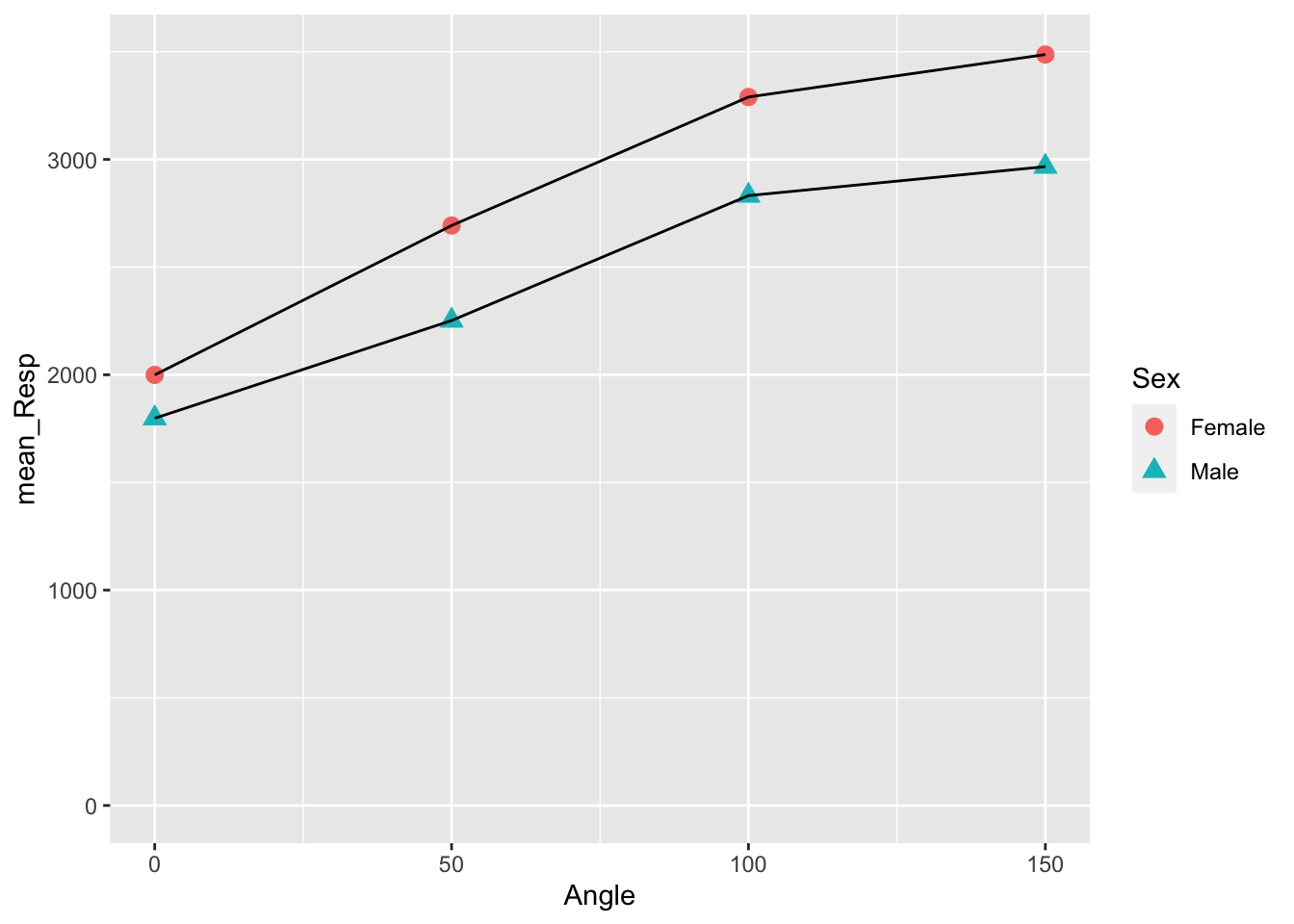
Changing Shape and Size of Data Points

Figure 3.10: Changing Shape and Size of Data Points

A quick point - in, out, what's the aes about?

Hopefully you are beginning to spot the difference between setting a call within aes() (which stands for aesthetics) and setting outside the aes(). Outside aes() means that all observations take the one value or color or type. Inside means that each observation within a condition takes the same value or color or type, but different conditions have different values/color/type

Let's look at what we have done above to help us compare.

size is called outside of the aes() and we assign it a specific value. As you can see from the Task 6 figure, each condition now has the same size of points. We could set this size to what we want but keep it smallish: 3 or 5 are ok; 50 would be artistic but not that informative.

In contrast, we called shape inside the aes() and we set it based on a variable, Sex. Doing it this way ensures that each level of the Sex variable, male or female, get a different shape.

Had we instead set shape outside the aes(), something like geom_point(shape = 3, size = 3) then all conditions would have the same shape and the same size. Different numbers relate to different shapes and different sizes. For example compare shape = 3 to shape = 13

Likewise, had we set the size within aes(), something like geom_point(aes(shape = Sex, size = Sex)) then both male and female would have different shapes AND different sizes. You can play around with this in your code to see how things work. And of course there are other arguments you could use. For example if you wanted all points to have the same color, say red for example, then you could do geom_point(color = "red"). Remember to put the quotes around the color.

So hopefully this is starting to make sense and you can think about implementing it in your own figures. Note that arguments are separated by a comma. e.g. geom_point(color = "red", size = 3, shape = 2)

3.3.8 Task 7: Adding Labels and Changing the Background

This figure is looking really nice now. Let's finish it off by making it look a little more professional with appropriate labels and by editing the background. We introduced these to you in the preclass so hopefully you had a play with them to see how they work.

To change a label, we use the labs() function and it works like labs(x = "Name", y = "Name", title = "Name").

  1. Add this function to your code so that the y axis indicates Mean Reaction Time (ms) and the x axis indicates Angle of Rotation (degrees). We haven't set a title here but you can if you want some practice. Titles on Psychology figures are not common. That said, a recent change to the APA style guide might change that!

  2. Set the figure as theme_bw() - this looks nice but there are other options you might want to try which you can explore through ?theme or the cheatsheet.

labs(x = "...", y = "...") + theme_bw()

The key thing is to remember to + the layer into the ggplot chain. And don't get this confused with pipes (%>%).

Note: You add (+) layers to figures, and you pipe (%>%) between functions.

3.3.9 Task 8: Separating a Variable and Removing Legends

Finally in the preclass we showed you two other functions that you could use to tidy up figures: facet_wrap() and guides().

  • facet_wrap() is really effective for splitting up figures into panels based on a variable; it works like facet_wrap(~variable) where ~ can be read as by. So "split up the figure by variable", for example Sex. And if you had two variables to split the figure by, then: facet_wrap(~variable1 + variable2).

  • guides() is handy for turning on and off legends which might be taking up space. For instance, if you use a facet_wrap() to split the panels into Female and Male, do you really need the legend on the right saying Female and Male? You will normally have a guide for all the color, shape, etc, calls you have in your pipeline within your aes() calls. It works like guide(call = FALSE).

  1. Add a facet_wrap() to have separate panels in your figure based on Sex.

  2. Turn off all guides so that you do not have a legend in your figure.

  1. facet_wrap(~variable)
  2. guides(group = FALSE, ???? = False, ....)


Group Discussion Point

If you have followed all the tasks correctly then you should have the following figure:

## `summarise()` has grouped output by 'Sex'. You can override using the `.groups` argument.
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.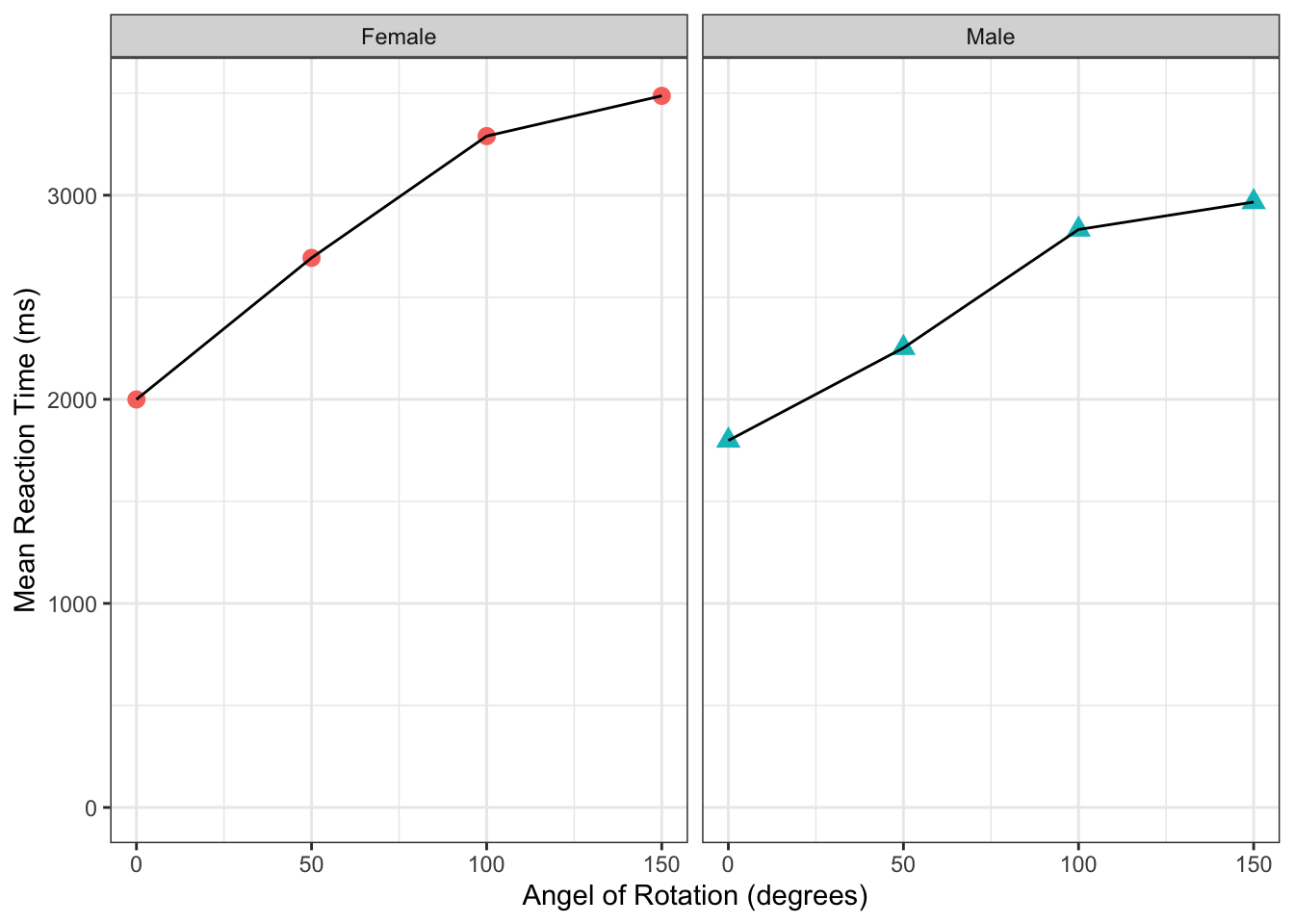
The finished figure!

Figure 3.11: The finished figure!

Take a few minutes with your partner or group to look at the figure and try to intepret it in terms of reaction time as a function of rotation and sex. Try answering the following questions to help your discussion:

  • In both sexes, mean reaction time angle of rotation.

  • Angle of Rotation influences more than

By looking at the figure, as angle of rotation increases (moving to the right of the x axis), the mean reaction time increases (getting higher on the y axis), indicating that participants take longer to respond the further the target image is rotated from the original. Also, as the male mean reaction times are quicker overall than the female mean reaction times, and the differences in reaction times between 0 degrees and 150 degrees is smaller in males, then you could perhaps say that males are affected less than females, or males perform the task quicker.

Keep in mind that we are only looking at correct responses here. As such, this figure would suggest the difference is not just male participants just responding quicker overall. Instead it may suggest that males are responding correctly quicker overall but you would need to take into consideration the difference in overall correct reponses between females and males which we saw in the preclass.

Differences in mental roration tasks have received much attention over the years and you should refer to the reference sections of the two main papers of this activity should you wish to follow the topic further and wish to add this to your Portfolio.

3.3.10 Additional Considerations (briefly!)

  1. Many of the options we have seen in terms of geom_point() could have been applied to geom_line() to make alterations to the line. Try playing with these options. For example, the code line below would result in both sexes having a red line of equal size but the style of line being different. Give it a shot!

geom_line(aes(linetype = Sex), size = .5, color = "red")

  1. Finally, if you look closely at the figure, you will see that the line between points actually goes in front of the points. It looks a bit messy. How could you make it tidier by having the line run behind the data points? Not sure? Remember that figures are constructed based on a series of layers. We draw one layer and then the next, so changing Task 8 to would draw the lines first and then the points on top. Give it a go!
ggplot(data = menrot_facet_guide, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_line() +
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  labs(x = "Angel of Rotation (degrees)", y = "Mean Reaction Time (ms)") +
  facet_wrap(~Sex) +
  guides(group = FALSE, color = FALSE, shape = FALSE) +
  theme_bw()

Job Done - Activity Complete!

In this chapter we have looked at working with layers and a variety of calls to shape, color, fills, etc, to create professional looking figures. Understanding figures through ggplot can seem like trial and error until you have a lot of experience. That is fine but just remember to keep adding notes to your Portfolio to help out the future you. And the beauty of it all is that once you have a figure you really like, you run the code and you get exactly the same figure again! Amazing or what???

You should now be ready to complete the Homework Assignment for this lab. The assignment for this Lab is summative and should be submitted through the Moodle Level 2 Assignment Submission Page no later than 1 minute before your next lab. If you have any questions, please post them on the available forums. Finally, don't forget to add any useful information to your Portfolio before you leave it too long and forget.

3.4 Assignment

This is a summative assignment and as such, as well as testing your knowledge, skills, and learning, this assignment contributes to your overall grade for this semester. You will be instructed by the Course Lead on Moodle as to when you will receive this assignment, as well as given full instructions as to how to access and submit the assignment. Please check the information and schedule on the Level 2 Moodle page.

3.5 Solutions to Questions

Below you will find the solutions to the questions for the Activities for this chapter. Only look at them after giving the questions a good try and speaking to the tutor about any issues.

3.5.1 InClass Activities

3.5.1.1 InClass Task 1

library("tidyverse")

menrot <- read_csv("MentalRotationBehavioralData.csv")
demog <- read_csv("demographics.csv")

Return to Task

3.5.1.2 InClass Task 2

menrot_angle <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_angle, aes(x = Angle, y = mean_Resp)) + 
  geom_point() +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)
  • coord_cartesian() is a function that can be used to show certain parts of a figure, controlling the visible X and Y axes. expand = TRUE adds a smaller buffer to the numbers you set. If you want to remove this buffer then set expand = FALSE.

Return to Task

3.5.1.3 InClass Task 3

menrot_angle_sex <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_angle_sex, aes(x = Angle, y = mean_Resp)) + 
  geom_point() +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)

Return to Task

3.5.1.4 InClass Task 4

menrot_grouped <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_grouped, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point() +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)

Return to Task

3.5.1.5 InClass Task 5

menrot_grouped_color <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_grouped_color, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex)) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)

Return to Task

3.5.1.6 InClass Task 6

menrot_shape_size <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_shape_size, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE)

Return to Task

3.5.1.7 InClass Task 7

menrot_lab_theme <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))

ggplot(data = menrot_lab_theme, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  labs(x = "Angel of Rotation (degrees)", y = "Mean Reaction Time (ms)") +
  theme_bw()

Return to Task

3.5.1.8 InClass Task 8

manrot_facet_guide <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))
## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.
ggplot(data = manrot_facet_guide, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  labs(x = "Angel of Rotation (degrees)", y = "Mean Reaction Time (ms)") +
  facet_wrap(~Sex) +
  guides(group = FALSE, color = FALSE, shape = FALSE) +
  theme_bw()
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.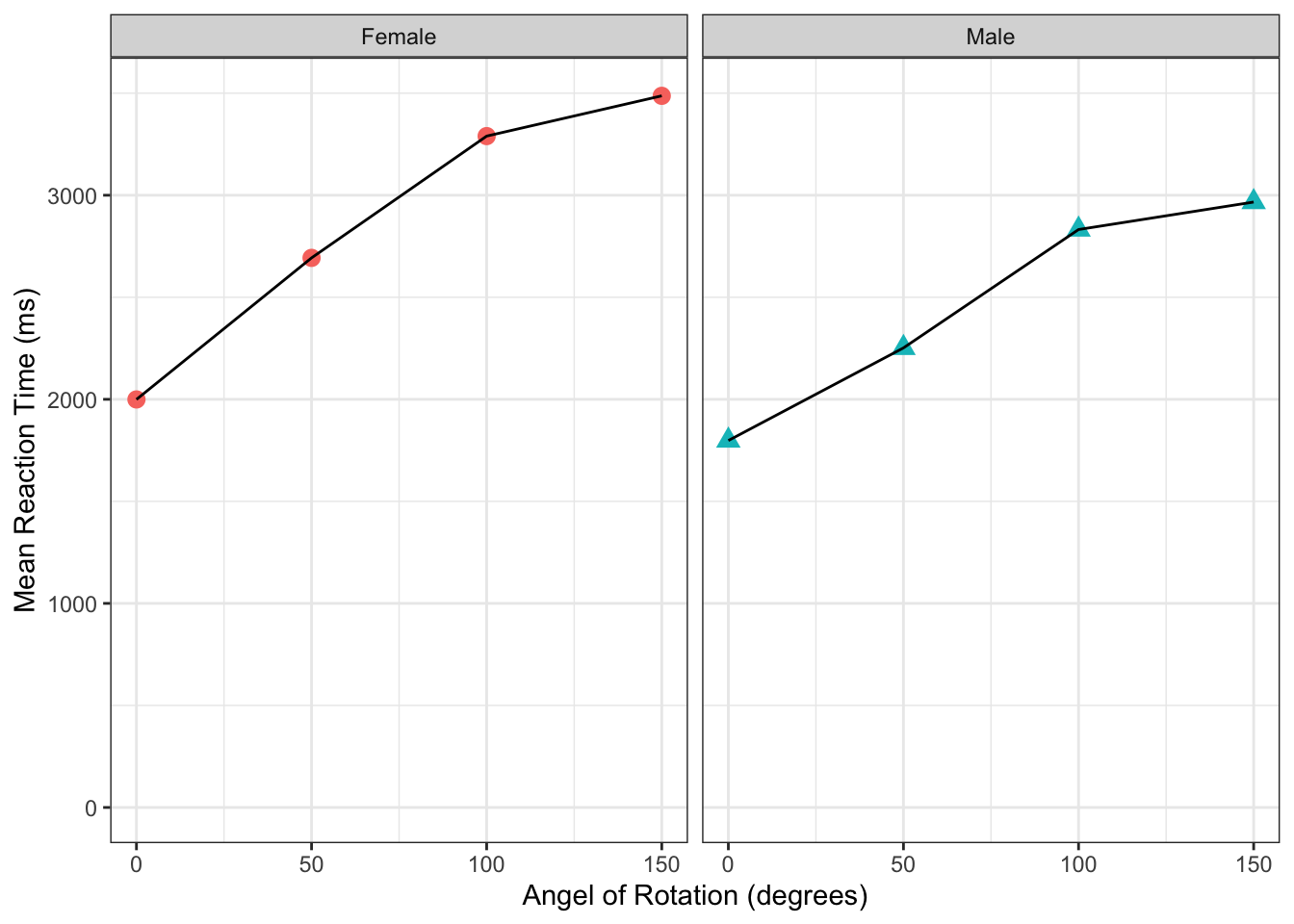
Task 8

Figure 3.12: Task 8

  • Remembering it is a layer system, we could use the below code to have the lines behind the points.
manrot_facet_guide <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))
## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.
ggplot(data = manrot_facet_guide, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_line() +
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  labs(x = "Angel of Rotation (degrees)", y = "Mean Reaction Time (ms)") +
  facet_wrap(~Sex) +
  guides(group = FALSE, color = FALSE, shape = FALSE) +
  theme_bw()
## Warning: `guides(<scale> = FALSE)` is deprecated. Please use `guides(<scale> =
## "none")` instead.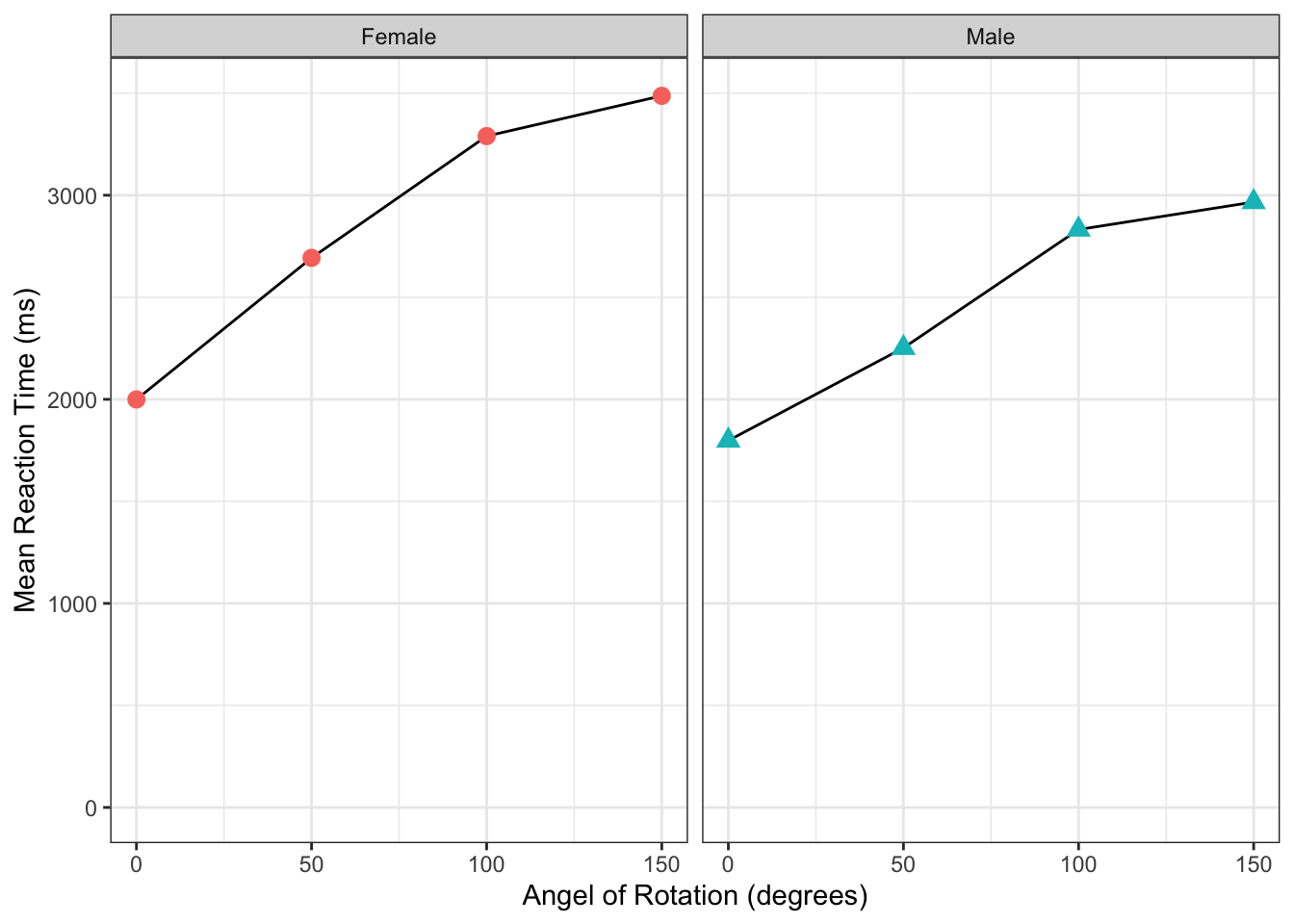
Task 8 Alternative

Figure 3.13: Task 8 Alternative

Return to Task

Chapter Complete!

3.6 Additional Material

Below is some additional material that might help you understand figures a bit more and how to present them in reports

More on aes() - when to and when not to!

The inclass activity has a short note about using the aes() call but we see people having issues with this so we thought a quick demonstration might help. Here is the code from the activity

menrot_angle_sex <- filter(menrot, CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant") %>%
  group_by(Angle, Sex) %>% 
  summarise(mean_Resp = mean(Time))
## `summarise()` has grouped output by 'Angle'. You can override using the `.groups` argument.
ggplot(data = menrot_angle_sex, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex, shape = Sex), size = 3) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  theme_gray()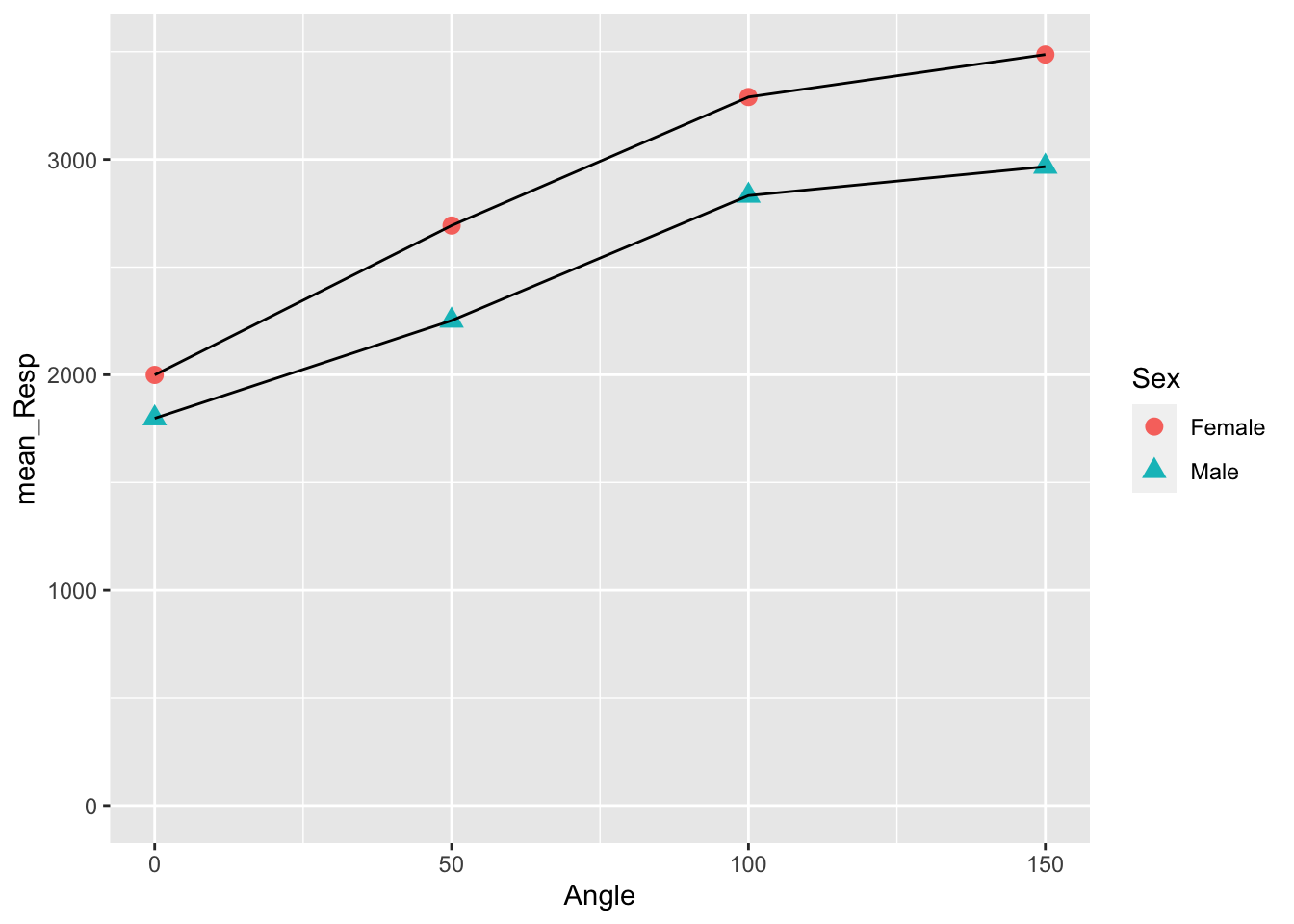
Changing Shape and Size of Data Points

Figure 3.14: Changing Shape and Size of Data Points

Specifically, we are going to focus on the geom_point() line. Inside the aes() we stated color = Sex, shape = Sex and outside the aes() we stated, size = 3. Earlier we said, outside aes() means that all observations take the one value or color or type. Inside means that each observation within a condition takes the same value or color or type, but different conditions have different values/color/type. So based on that understanding, in the above plot, all shapes have the same size (i.e. 3), but there is a different shape and color of shape for each sex. Now let's demonstrate some alternatives.

  1. All points have the same shape, color and size - nothing is in an aes().
    1. here we need to state the color, shape and size we want all observations to have. We have chosen red for color (in quotes) shape style 3 (+) and size 6. We are not using a variable to split observations into groups.
    2. we have changed the size to make the visualisation clearer
ggplot(data = menrot_angle_sex, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(color = "red", shape = 3, size = 6) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  theme_bw()
All points have the same shape, color and size

Figure 3.15: All points have the same shape, color and size

  1. All points have the same shape and size but color is determined by Sex (so goes inside the aes()).
    1. here we need to state the shape and size we want all dots to have. But this time we are giving the different levels within Sex (i.e male and female) different colors - by putting that inside the aes()
ggplot(data = menrot_angle_sex, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex), shape = 3, size = 6) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  theme_bw()
All points have the same shape and size but color is determined by Sex

Figure 3.16: All points have the same shape and size but color is determined by Sex

  1. We showed the code for setting color and shape by Sex previously. Instead now we will set the color, shape and size by the variable Sex.
    1. here as all options are in the aes() we will have different colors, sizes, and shapes between males and females, but all males will have the same color, size and shape, and all females will have the same color size and shape.
ggplot(data = menrot_angle_sex, aes(x = Angle, y = mean_Resp, group = Sex)) + 
  geom_point(aes(color = Sex, shape = Sex, size = Sex)) +
  geom_line() +
  coord_cartesian(ylim = c(0, 3500), expand = TRUE) +
  theme_bw()
## Warning: Using size for a discrete variable is not advised.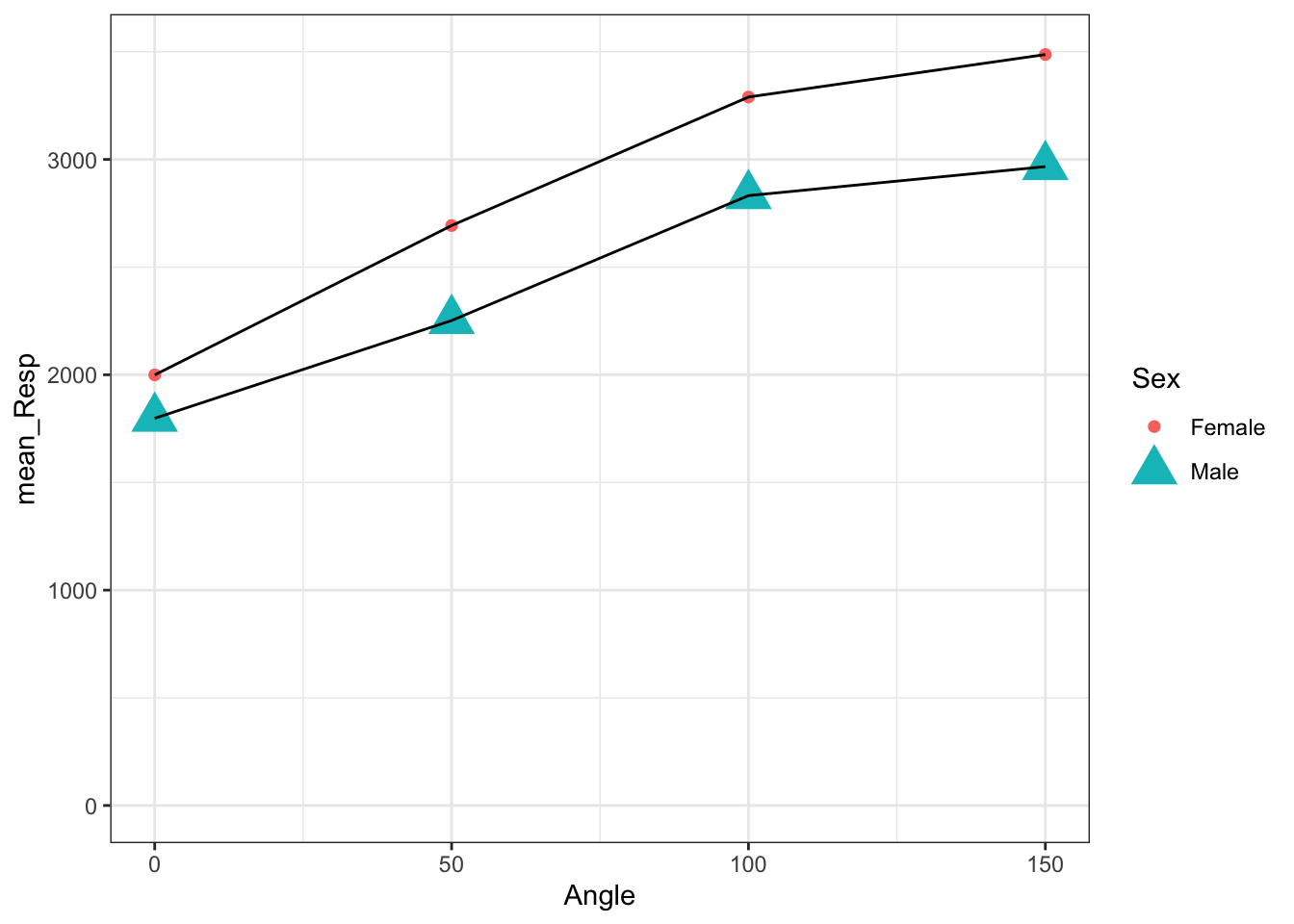
All points have the same shape and size but color is determined by Sex

Figure 3.17: All points have the same shape and size but color is determined by Sex

You actually get a warning when doing this option. Why? Because if you had numerous options then you would have too many different shapes being created and it would cause issue with the code and may even crash it. Pay attention to warnings.

And the reason you have to decide what is the best approach for displaying your data is because if all observations within a condition are the same, then showing them as all different colors and shapes makes very little sense. You always need to think about what you are trying to convey. Look at these two figures and think about which one is easier to understand that all observations are from the same condition. The one on the left! The one on the right suggests there is something different about all the observations.

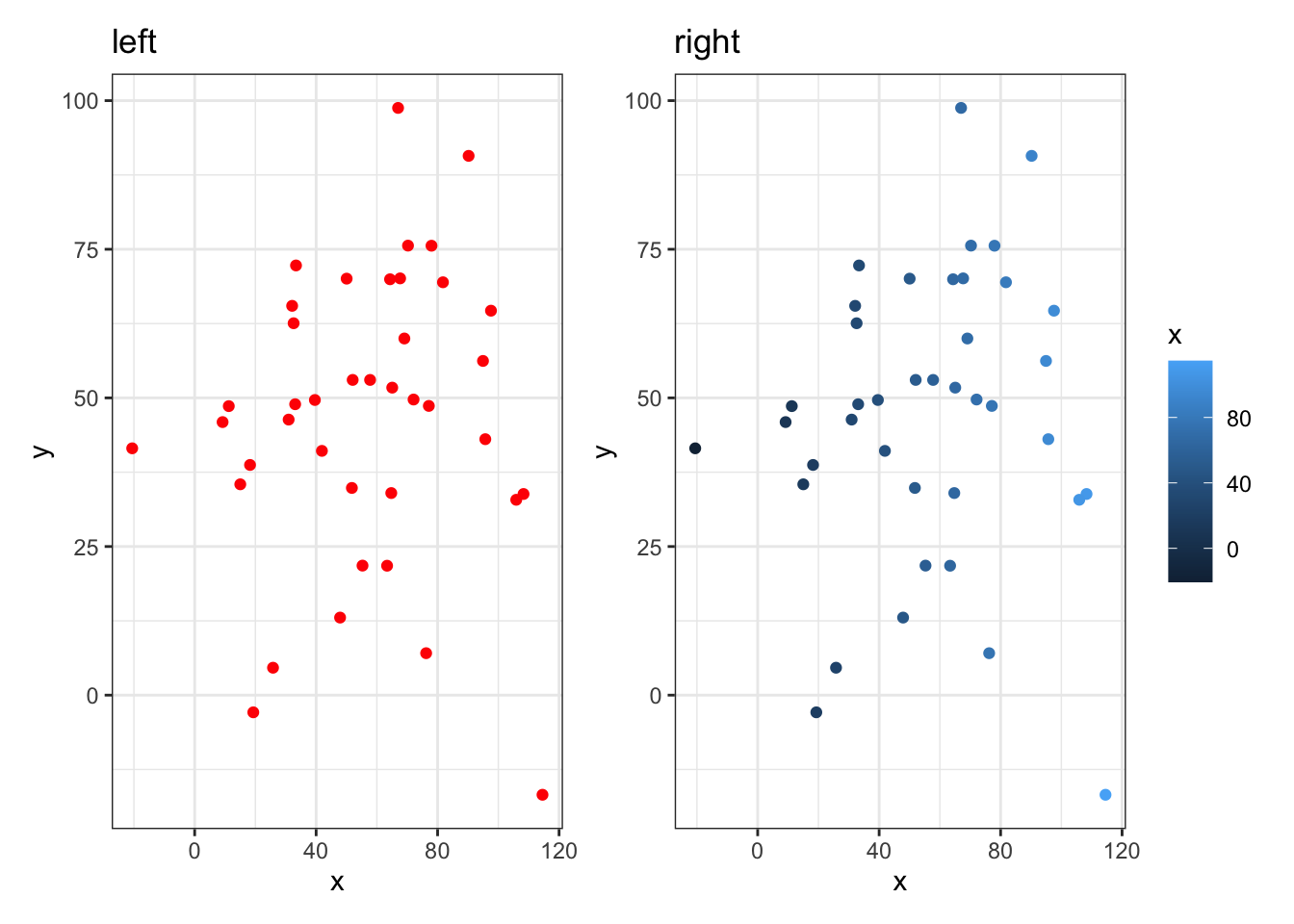
The plot on the left suggests all observations are of the same condition. The figure on the right suggests a difference between all observations. Always think about what your information you convey in your figures!

Figure 3.18: The plot on the left suggests all observations are of the same condition. The figure on the right suggests a difference between all observations. Always think about what your information you convey in your figures!

Hopefully that is beginning to become clearer. Insider the aes() means that all observations within a variable/condition are shown the same, but are different from observations from a different variable/condition. Outside the aes() means that all observations are shown as the same regardless of condition.

Combining Plots into one Figure

Space within a report is a commodity. Figures can be incredibly useful in getting information across in a very efficient manner, but when you have a strict word count, having multiple figures can really chew into the limit, given that each figure needs a legend and each legend counts. One way to get around this is to merge figures together into one big figure that perhaps convey similar or related information. We are going to show you how to do that using a package called patchwork.

DO NOT install packages in the Boyd Orr labs; most are already there and just need called in through library(). If it is not there, speak to a member of the team.

patchwork is unlikely to be on our lab machines so please only try this on your own machine. If you haven't previously installed the patchwork package on your own machine before, you will have to install it first, e.g. install.packages("patchwork").


Thinking back to the preclass, plots like boxplots and histograms, when combined, can be incredibly useful in understanding the overall shape of your data and whether or not it fits the assumptions of inferential tests, something we will come on to later. If we were to create two separate plots, we might get something like this:

menrot_hist_correct <- group_by(menrot, Participant, CorrectResponse) %>% 
  summarise(Mean_Time = mean(Time, na.rm = TRUE)) %>%
  filter(CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant")

ggplot(data = menrot_hist_correct, 
       aes(x = Mean_Time,
           fill = Sex)) + 
  geom_histogram() +
  theme_bw()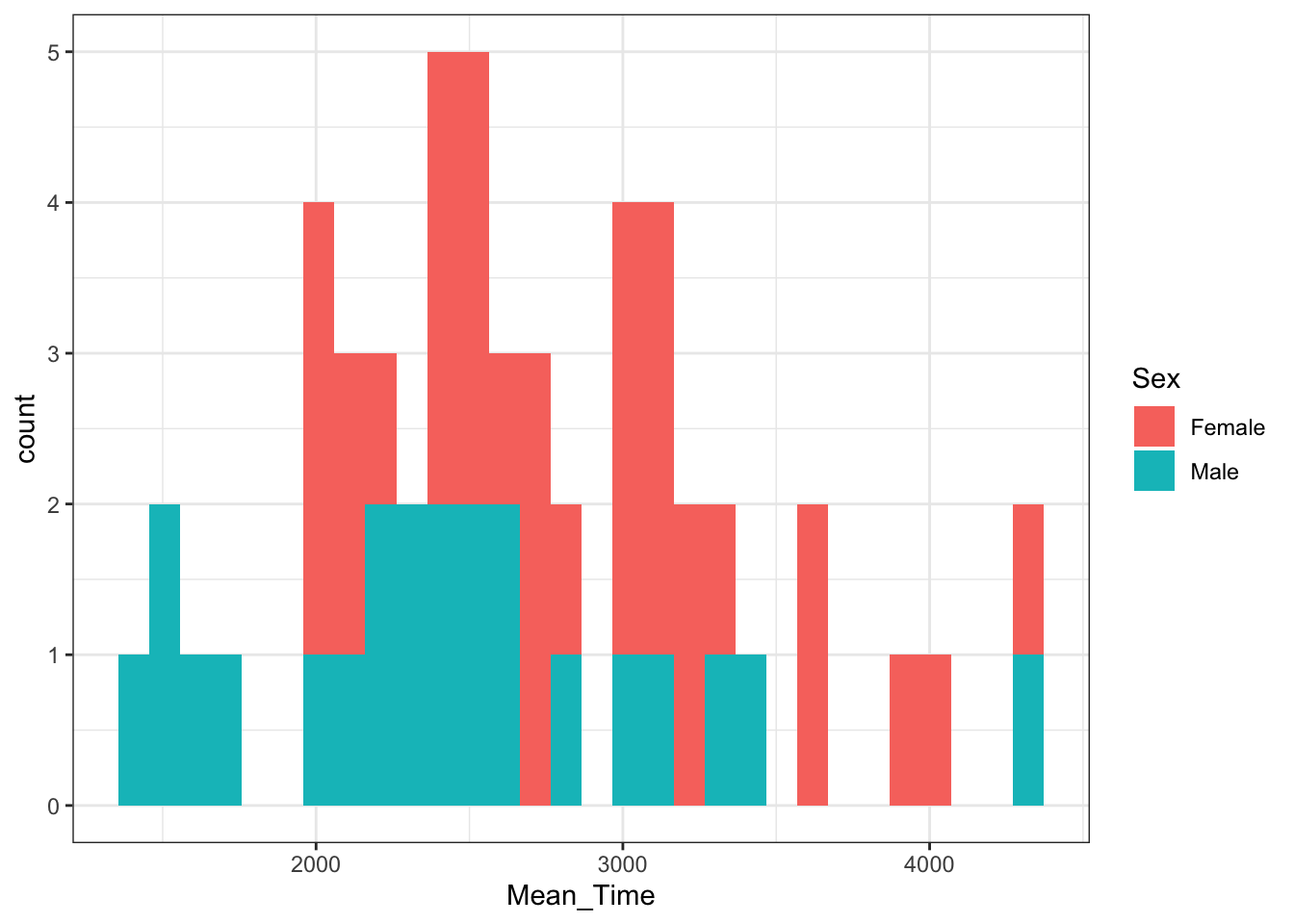
A histogram of distribution of Mean Time counts by Sex

Figure 3.19: A histogram of distribution of Mean Time counts by Sex


And:

menrot_box_correct <- group_by(menrot, Participant, CorrectResponse) %>% 
  summarise(Mean_Time = mean(Time, na.rm = TRUE)) %>%
  filter(CorrectResponse == "Correct") %>%
  inner_join(demog, "Participant")
## `summarise()` has grouped output by 'Participant'. You can override using the `.groups` argument.
ggplot(data = menrot_box_correct, 
       aes(x = CorrectResponse, 
           y = Mean_Time, 
           fill = Sex)) + 
  geom_boxplot() +
  theme_bw()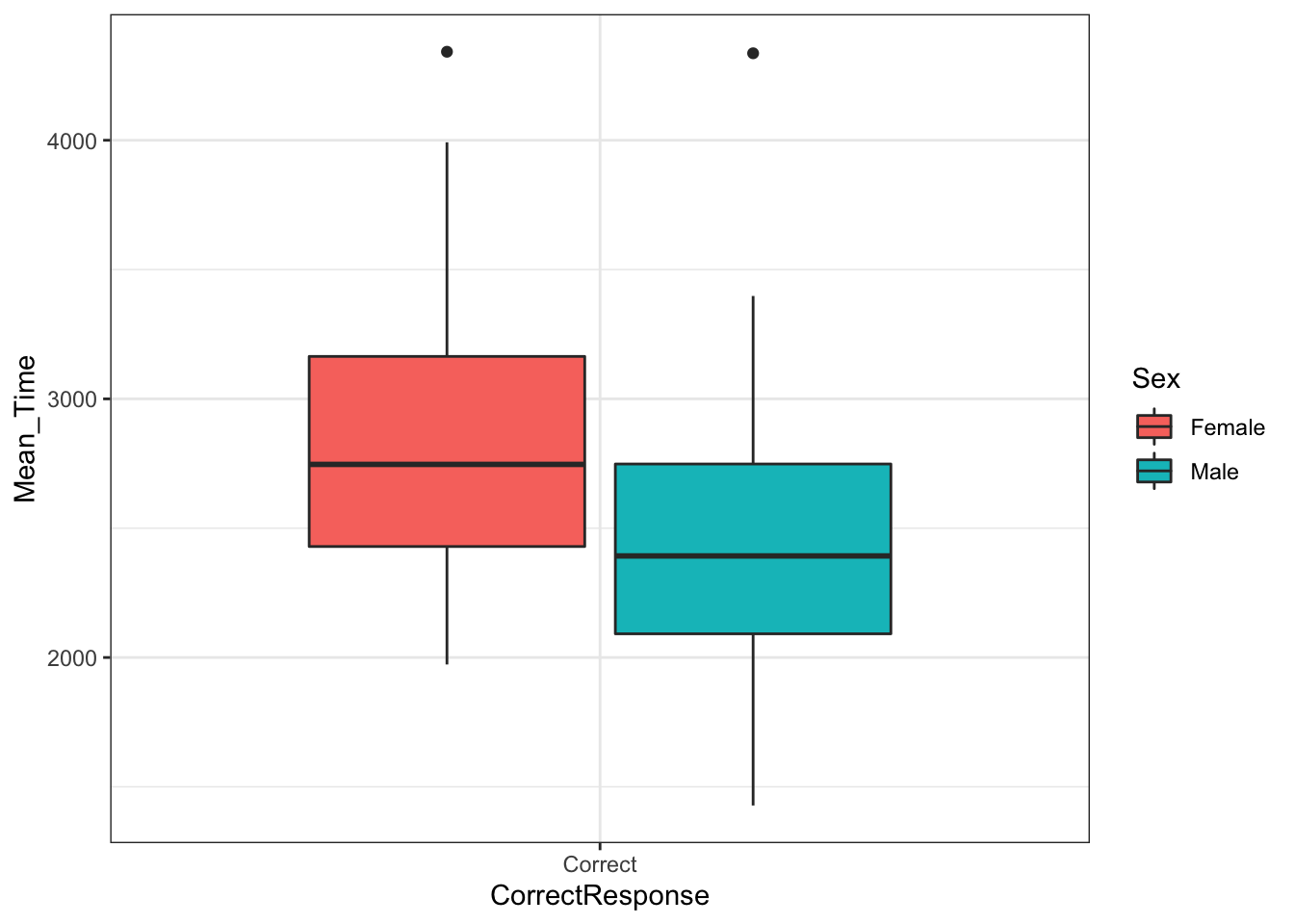
A boxplot of the spreads of Mean Time for Correct Responses by Sex

Figure 3.20: A boxplot of the spreads of Mean Time for Correct Responses by Sex


Now given that they both divide the data by sex, you can start to see how the figure legend for each plot becomes a bit repetitive, and how combining them into one figure would potentially make things easier. There are a number of packages to do this, but patchwork is very straightforward and flexible.

Let's now call in patchwork

library(patchwork)

The first thing you need to do when using patchwork is save your plots in an object (just like you would with the output of any function). Using the code above, this might look like below for the boxplot:

p_box <- ggplot(data = menrot_box_correct, 
       aes(x = CorrectResponse, 
           y = Mean_Time, 
           fill = Sex)) + 
  geom_boxplot() +
  labs(title = "A") +
  theme_bw()

And below for the histogram:

p_hist <- ggplot(data = menrot_hist_correct, 
       aes(x = Mean_Time,
           fill = Sex)) + 
  geom_histogram() +
  labs(title = "B") +
  theme_bw()


Note: The reason for the inclusion of a title on each plot will become clear in a second.

Note: When you run these codes no plots will be generated as you are saving them as objects - the boxplot in p_box and the histogram in p_hist. It is important to realise this distinction as if someone asks you to make produce a code where the figure is generated when your code knits, and you have saved your plot as an object, then your figure might not show. If you have save a plot as an object, you can generate the figure by just calling the name of the object. If you look at the ggplot cheatsheet you will see this approach a lot. Here is how we would call the boxplot stored in p_box.

p_box
A boxplot of the spreads of Mean Time for Correct Responses by Sex

Figure 3.21: A boxplot of the spreads of Mean Time for Correct Responses by Sex 

p_hist
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.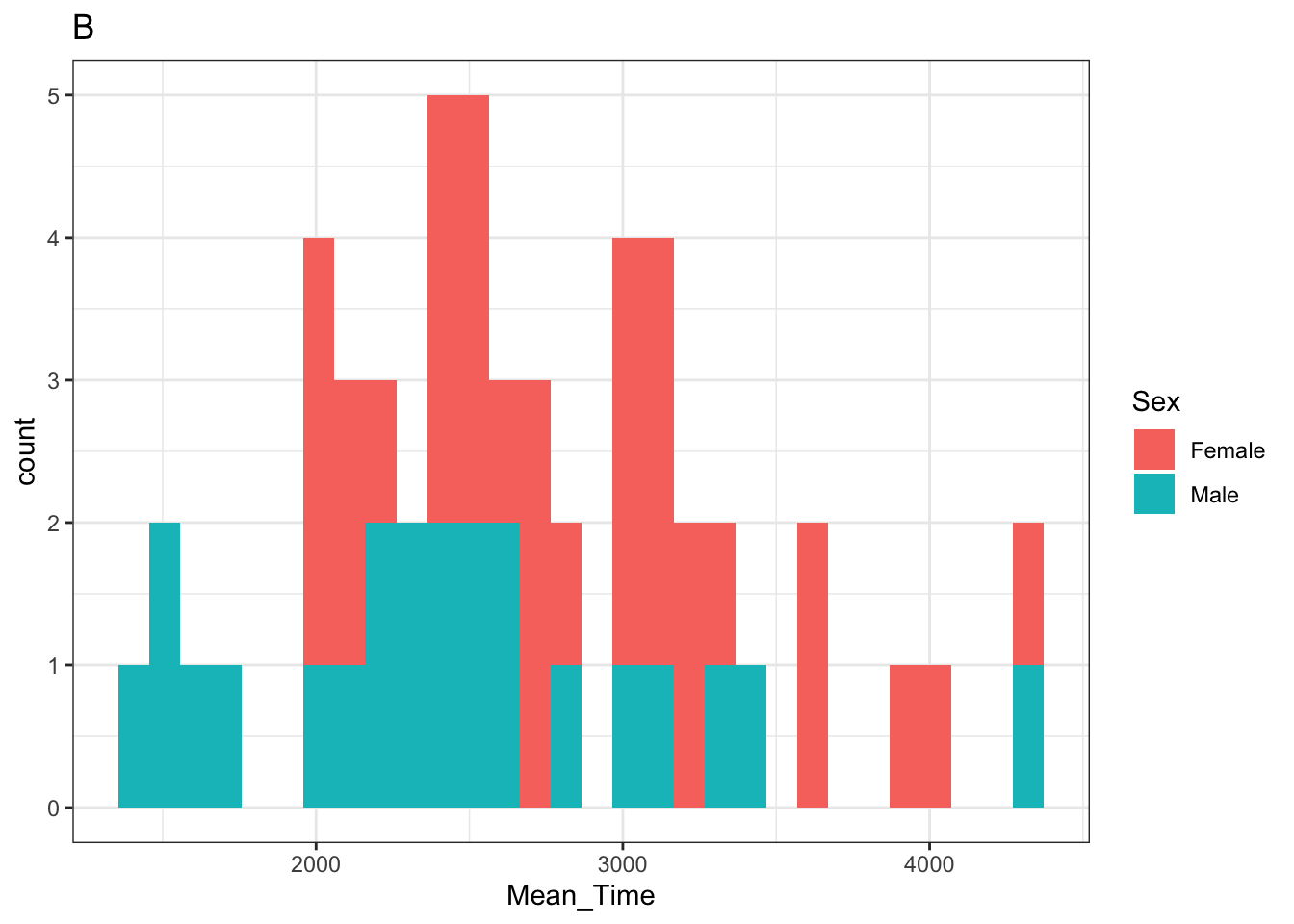
A histogram of distribution of Mean Time counts by Sex

Figure 3.22: A histogram of distribution of Mean Time counts by Sex


Note: You will see a warning from the histogram plot about selecting a binwidth. We haven't really looked at this yet but will do in due course. If you wanted to "fix" that warning then changing the histrogram code to something like + geom_histogram(binwidth = 100) might work. The value that you enter is relative to the scale of your data. A binwidth of 1 would create a bin every increase of 1 ms. A binwidth of 100 creates a bin every 100 ms.

So far so nothing exciting. Looks just like what we have seen in the lab. Didn't we say we wanted both the plots in a single figure, right? Well to do that in patchwork, we simply "add" the plots together using a plus sign (+), as such:

p_box + p_hist
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.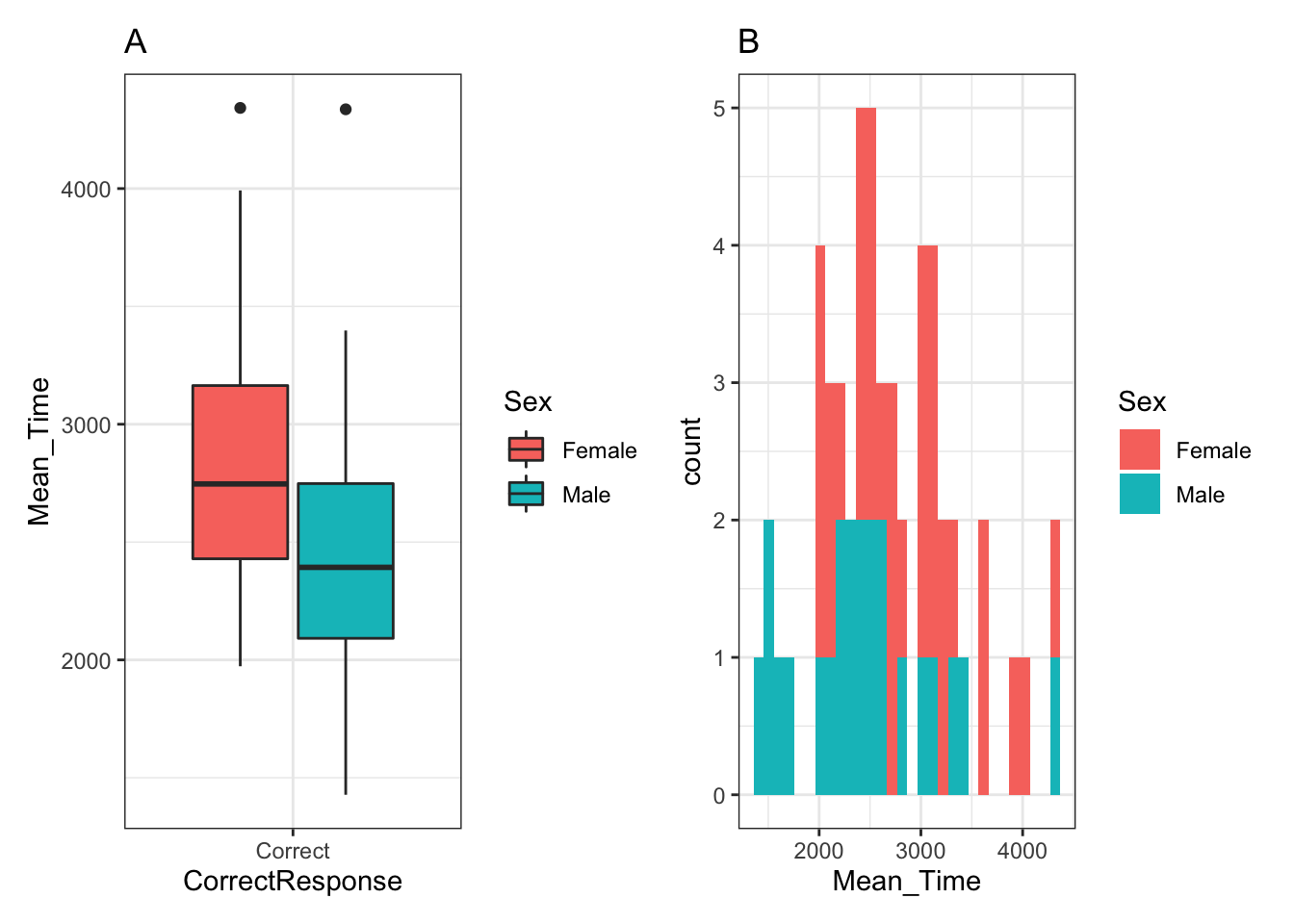
A boxplot (A - left) of the spreads of Mean Time for Correct Responses, and histogram (B - right) of distribution of Mean Time counts, both separated by Sex (female - red, male - cyan)

Figure 3.23: A boxplot (A - left) of the spreads of Mean Time for Correct Responses, and histogram (B - right) of distribution of Mean Time counts, both separated by Sex (female - red, male - cyan)

Note: We can use the "titles"" we added to the plots in the original code above to tell readers which plot, within the combined figure, we are referring to, A or B, left or right, as shown in the figure legend beneath the figure. This might seem a bit pedantic, but you have no control over how somebody views your published figure, and as such clarity is paramount!

Awesome, that it? No! We can also change the configuration of the plots in the combined figure. Say we wanted the plots on top of each other - portrait rather than landscape - well in that instance we divide the plots using the divide sign (/), as such:

p_box / p_hist
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.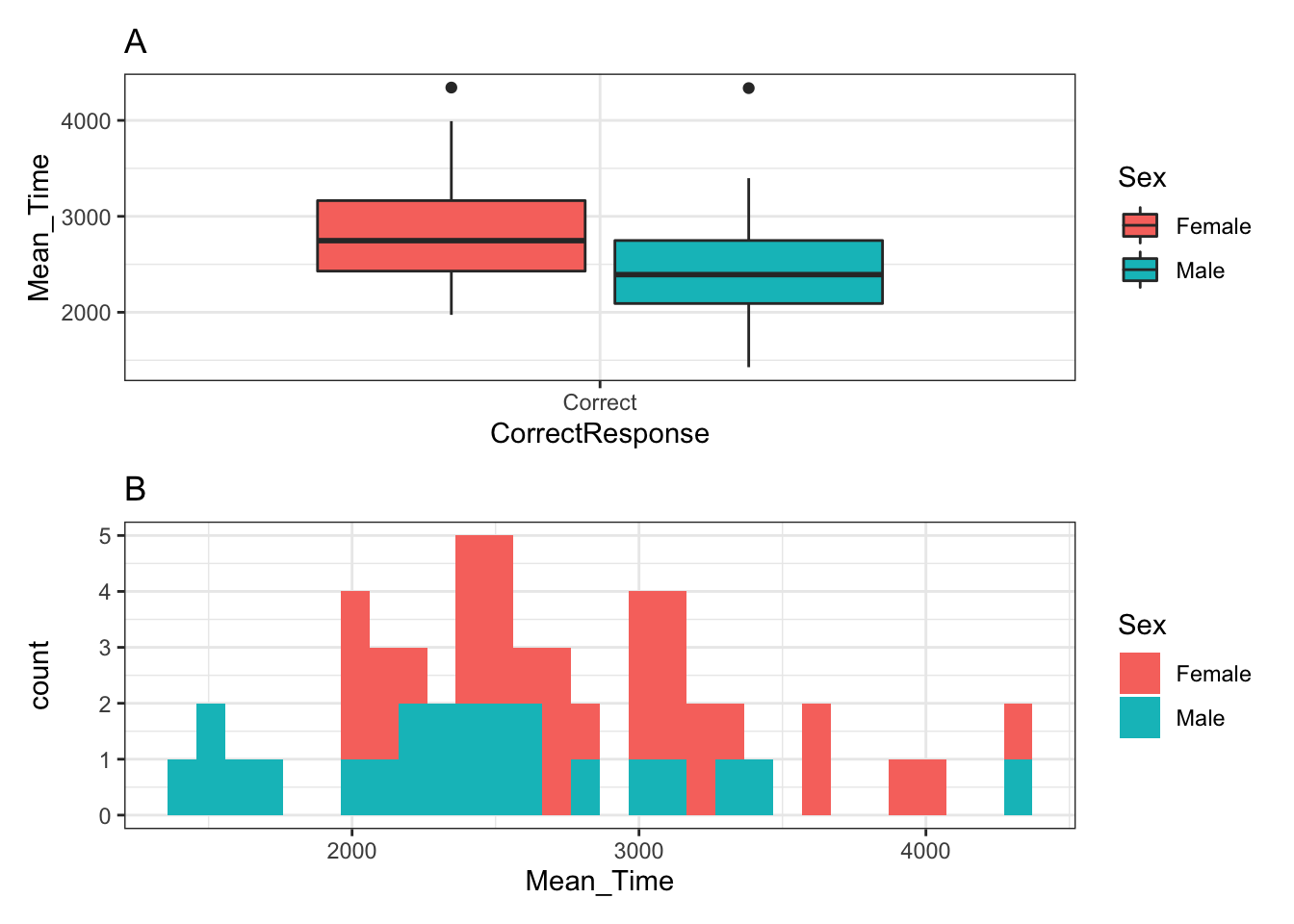
A boxplot (A - top) of the spreads of Mean Time for Correct Responses, and histogram (B - bottom) of distribution of Mean Time counts, both separated by Sex (female - red, male - cyan)

Figure 3.24: A boxplot (A - top) of the spreads of Mean Time for Correct Responses, and histogram (B - bottom) of distribution of Mean Time counts, both separated by Sex (female - red, male - cyan)

And now we refer to top and bottom, rather than left and right. In fact, patchwork is really flexible and can work with multiple plots and arrangements. Hypothetically, say you had three plots and wanted two on top of one, then you would use the approach of combining "+" and "/" as such:

(plot1 + plot2)/plot3

Remember the trick to using patchwork is to save your plots as objects first (p1 <- ggplot(....)) and the rest is easy. But be sure to always know if your figure is to be shown when knitted or not; more often than not, seeing the figure is more important than seeing the code.

Happy Visualising!

End of Additional Material!